場の古典論《32節》エネルギー・運動量テンソル
▷ラグランジアン密度と最小作用の原理
▷電磁場のラグランジアン密度Λの場合
▷エネルギー・運動量密度テンソルの導出
▷場のエネルギー運動量テンソルTikに係る保存則
▷粒子系のエネルギー運動量テンソル
▷場のエネルギー運動量テンソルの解析の再開
▷テンソルφikmを微分した項の追加
▷角運動量テンソルの保存
【場の古典論】
【第4章】場の方程式
【第32節】エネルギー・運動量テンソル
《ラグランジアン密度》
x方向の「ひも」のy方向の運動をあらわすことを考える。質量M/nを持ったn個の物体がx方向の長さaのバネでつながれて並んでいる。この鎖状の構造体は左右から張力Tで引っ張られているとする。この中の質点の一つだけをy方向の上か下に少しだけ移動させた場合を想像する。物体間の距離がaであり,物体が上にdyだけ移動したとする。dyがaに比べて極めて小さい場合は張力はTとほとんど変わらない。「ひも」の張力のベクトルのy方向成分を考える。

dyがaより十分小さい時には点Bをy方向へ動かすために点Aから働く力は-T(dy)/(a)であると言える。その逆に、点Bから点Aに対して力が働くとも言える。dyが0に近いと力が働かない。dyの2乗に比例したエネルギーが点AB間のバネに蓄えられると言える。それから、以下のラグランジアンLが考えられる。

第 1 項は「全質点の運動エネルギー」である。第 2 項目は張力の項である。隣どうしの質点の,それぞれの変位の差をYとしたとき,Yに比例した復元力-kYが働く。ここで書いた係数kの正体はT/aである。
次に、y(x,t)は連続関数であると考え、x軸に沿って連続的に和を取る積分記号に置き換える。aをdxと全く同じものだと見なす事で対応する。

この最後の式の積分の中身は「ラグランジアン密度」Λと呼ばれている。

このようにして一旦ラグランジアン密度Λを求めることができたならば、以下の、「場の古典論」32節の計算方法によって、速やかにラグンランジュ方程式(32.2)を得ることができる。
《32節の議論の大前提》
先ず、空間が一様かつ等方的であり、時間も一様である性質を持った慣性系で記述することを大前提にして考える。
空間と時間の一様性は、ラグランジアンが3次元座標の変数と時間の変数をあらわには含まない(循環座標)ことを意味する。空間の等方性は、ラグランジュアンが4次元空間の回転角度にかかわる変数をあらわには含まない(循環座標)ことを意味する。
最小作用の原理を用いて場の方程式を求めるには、
以下の作用積分S、すなわち、ラグランジアン密度Λの積分Sを求める。ラグランジアン密度Λは、一般化座標(系のパラメータ)の一種の、場のベクトルポテンシャルの成分などの場のパラメータqと、そのパラメータqの4次元座標方向での微分量q,i のパラメータであらわす。パラメータq,i は、ラグランジアンLをあらわすパラメータの1つの、一般化座標qの時間微分(速度)に対応する。すなわち、ラグランジアンLでの時間軸の方向を、ラグランジアン密度Λでは全ての4次元座標方向に拡張して対応させる。
このように、慣性系を記述する一般化座標のパラメータとして、4次元座標の関数の場のパラメータqを用いる。更に、複数の粒子の各々の3次元座標の変数xk と時間の変数tも併用する。ただし、ラグランジアンLが3次元座標の変数xk と時間の変数tをあらわには含まない(循環座標)ので、ラグランジアン密度Λは、3次元座標の変数xk と時間の変数tのパラメータをあらわには含まない。ここでは、更に、粒子(電荷)の無い場合を考えることにして、ラグランジアン密度Λには、3次元座標の時間微分=粒子の速度vk のパラメータもあらわには含ませないことにする。

この作用積分Sに対して最小作用の原理を適用する。
(なお、上記の式では表示の簡単化のために、複数個の場のパラメータを1つのパラメータqだけで表して、他のパラメータを省略している)
「場の古典論」では、作用積分の領域の時間的境界面に、場のqを固定している。最小作用の原理を適用するイメージとして、下図のx,y,z,tの4次元空間(z軸は図示しない)内の場のパラメータqを考える。

この4次元空間の時間軸方向の大きさは、時間軸方向での最初の時刻と最後の時刻との間の時間Δtの大きさを持つ。この4次元空間の3次元空間座標軸方向の大きさは、時間軸方向の大きさΔtの光速度 c 倍のcΔtよりも十分に大きく、ほぼ無限遠に至るまで大きくする。場は光速度で伝わるので、場の存在する領域から光速度で達する領域よりも外の領域には場のパラメータqが存在しない。すなわち、4次元空間の3次元空間座標軸方向の十分に遠方の端では場のパラメータqが存在しない。そのような4次元的な直方体の領域を考える。
その4次元的な直方体の時間軸方向での4次元的な境界面(与えられた最初の時刻での3次元空間と、Δt後の最後の時刻での3次元空間)に、場のパラメータqが固定されている。
ラグランジアン密度Λを、場のパラメータqと、その4次元座標方向での微分量のパラメータq,i を使ってあらわす。 そして、上図の4次元的な直方体内のラグランジアン密度Λを積分して電磁場の作用積分Sを求める。
その作用積分Sの値が最小になるように、場のパラメータqの、各時刻と各位置における値を定める。
その作用積分Sの変分δSが以下の式で計算できる。

次に、第1項の積分にガウスの定理を適用する。


先ず、第1項での4次元的境界面のうち、3次元座標の積分の限界である、3次元空間でほぼ無限遠方の4次元的境界面の位置では、場のパラメータqはゼロである。
次に、第1項での4次元的境界面のうち、時間方向の積分の限界の4次元的境界面は、与えられた最初の時刻の3次元空間(4次元的境界面)と、最後の時刻の3次元空間(4次元的境界面)である。それらの4次元的境界面においては、場のパラメータqがその4次元的境界面(3次元空間)に固定されている。そのため、その時間方向の4次元的境界面(3次元空間)では、qの変分δqがゼロである。
3次元空間の無限遠方での4次元的境界面においても、最初の時刻および最後の時刻での4次元的境界面においても、第1項の被積分関数が0になる。そのため、第1項が消えて以下の式になる。

最小作用の原理による変分δqは任意であるから、δqの係数をゼロに等しいとおかなければならない。結局、次の”運動方程式=ラグランジュ方程式”、すなわち場の方程式:

が得られる。この式(32.2)は、(ラグランジアンLの速度vでの偏微分であらわされる)一般運動量の時間微分が、(ラグランジアンLの一般座標での偏微分であらわされる)力Fになることをあらわすラグランジュ方程式に対応する。
このラグランジュ方程式(32.2)を最小作用の原理により変分法で求める手順は、第30節の変分法で、一般座標qを(場のパラメータ)にし、 δ(場のパラメータ)を掛けている式を取り出してラグランジュ方程式とするのと同じく、δ(場のパラメータ)を掛けている式を取り出して場の方程式を得た。第30節では、ラグランジアン密度Λの内容が定まっていたが、32節では、ラグランジアン密度Λの内容が定まっていない場合にも、ラグランジュ方程式(32.2)が求められた。このラグランジュ方程式(32.2)は、場のラグランジアンに限定されず、一般座標の関数の密度分布を持つ粒子系のラグランジアンにも適用できる。
《電磁場のラグランジアン密度Λの場合》
以上でラグランジュ方程式(32.2)を得た。以下では、電磁場のラグランジアン密度Λを、このラグランジュ方程式(32.2)に代入して電磁場の方程式を再現してみる。



以上の計算により、方程式(32.2)のラグランジアン密度Λに具体的な電磁場のラグランジアン密度Λを代入すれば、第30節の計算結果と同じ電磁場の方程式が得られることが確認できた。
《量子力学の電子場の方程式についても電磁場と同様》
量子力学のディラック方程式の解説を見ると、(ディラックの波動関数の確率密度が、ローレンツ変換される4元ベクトルを構成する(7.127))。その4元ベクトルである確率密度の場を、電磁場の4元ベクトルの場Aに対応させて電磁場と同様に確率密度の場に係るラグランジアン密度Λを導出できると考える。そのラグランジアン密度Λを使って、電磁場の方程式と同じような、電子の波動関数の確率密度の場の方程式を求めることができると考える。
《エネルギー・運動量密度テンソルの導出》
ラグランジュ方程式(32.2)を利用して以下の計算を行なう。ラグランジアンLの空間座標xでの微分が力Fである。Λがラグランジアンの密度なので、Λの空間座標xでの微分が力f(それは一般加速度ωに比例する)の密度に関係する。また、Λの時間tでの微分は、力のする仕事の密度に関係する。それらの量を計算していく。



こうして、ラグランジュ方程式(32.2)から、式(32.3)で定義されるテンソルTを使った4次元の発散が0になる方程式(32.4)が導き出せた。
ラグランジアンLの(dq/dt)=vによる偏微分は運動量pになる。ラグランジアンLでの時間軸tの方向を、ラグランジアン密度Λでは全ての4次元座標方向に拡張して対応させるため、Λの(∂q/∂(xk))による偏微分はLの(dq/dt)による偏微分に対応し、その偏微分結果は運動量密度に対応すると考えることができる。そう考えると、テンソルTの式(32.3)は、「力学」40節で、ラグランジアンLを使ったハミルトニアンHの式(40.2)に似ている。 そのため、このテンソルTは、ハミルトニアンHに対応する、エネルギー・運動量密度のテンソルに相当すると考えることができる。以下で、このテンソルTを元にしたエネルギー・運動量密度テンソルを定義していく。
《場のエネルギー運動量テンソルTikに係る保存則》
4次元の発散が0になる方程式(32.4)から、場のエネルギー運動量テンソルTik に係る保存則(エネルギー保存則と運動量保存則)が導き出されるをことを以下で示す。
既に最小作用の原理によって場のラグランジュ方程式が得られている。そのため、以下では、座標の関数として表されているラグランジアンや作用や場の量、式(32.4)の項の量を扱う計算をする。 4次元空間において、式(32.4)の項を4次元体積積分した式をガウスの定理で変換することによってテンソルTに係る保存則が導き出される。
32節では、この4次元空間での積分領域は29節での積分領域と同じであると示唆している。また、29節の積分は、最小作用の原理を適用するための積分では無く、既に得られた場の方程式に従う場を4次元空間で積分変換しているのである。32節で29節のどの説明を指摘しているか、あいまいでわかりにくい。32節の意図は、式(32.4)のように4次元発散が0になる場合には、29節で簡単に説明されたネーターの定理の手順に従うと保存法則が導出できることを指摘しているのである。そのため、以下で、29節で簡単に説明されたネーターの定理の手順に従い、式(32.4)から保存法則を導出する。先ずは、その4次元空間での積分の領域の定義を詳しく説明する。
その4次元空間の積分領域は、下図のように、時刻tが概ねaである、時間軸方向に概ね垂直な第1の4次元的境界面と、時刻tが概ねbである、時間軸方向に概ね垂直な第2の4次元的境界面と、それ以外に、空間座標が無限遠方の空間座標方向の6つの境界面で囲まれる4次元領域で積分する。

ここで、ラグランジアン密度Λが、座標の関数として与えられているということを前提に計算する。そのラグランジアン密度Λは無限遠では0であるものとする。第1と第2の4次元的境界面では各々、その4次元的境界面上の任意の2点の世界間隔は空間的であるものとする(ただし、境界面上で局所的な2点の間の世界間隔が時間的であっても良いものとする(この例外条件が、この4次元的境界面の説明を難しくしている))。そして、その空間的な4次元的境界面は、3次元空間方向では無限に広いものとする。その空間的な4次元的境界面の微小部分をdSk であらわす。
(空間的な4次元的境界面(超曲面))
第1と第2の境界面(超曲面)が空間的であるという意味は以下の意味である。すなわち、3次元空間内の全ての粒子の世界線がその4次元的境界面に交差し、その世界線が境界面の過去側から未来側まで通過するように、4次元空間に配置した境界面が空間的な超曲面である。
第1と第2の空間的な4次元的境界面(超曲面)での積分は3次元体積での積分である。第1の4次元的境界面での微小部分d(Sk)の3次元体積積分の結果は、第2の4次元的境界面での微小部分d(Sk)の3次元体積積分の結果に等しい。そのように空間的な4次元的境界面での超面積分である3次元体積積分の値が同じ値に保存される。それを以下の解析(ネーターの定理の手順)で導き出す。

この式の右辺を、以下のガウスの発散定理の式に代入する。

0=右辺の式から、以下の結果が得られる。先ずは、空間的に無限遠方では、場が存在しないので、Tik が0になるものとする。

すなわち、第1の空間的な4次元的境界面での体積積分d(Sk)と、第2の空間的な4次元的境界面での体積積分d(Sk)が等しい。空間的な超平面での積分(体積積分)が保存する。
第1の空間的な4次元境界面と第2の空間的な4次元境界面とは、時間方向で隔たっている。そのため、その境界面での積分の値が、時間を隔てても変らないことになる。すなわち、境界面での積分の値は時間の経過にかかわらず保存されるという保存則が存在することをあらわす。
この保存量の式は以下の式に整えることができる。

上の式は時間軸に垂直な超平面での積分である。下の式は、4次元空間で凹凸のある空間的な超曲面での積分である。空間的超曲面とは、x座標方向とy座標方向とz座標方向では無限遠までの広がりがある、空間的な4次元的超曲面(微小領域dSk≒dS0)の領域での体積積分である。
このベクトルPi は、系の運動量の4元ベクトルと同一のものとみなされなければならない。われわれは、以前の定義にしたがって、この4元ベクトルPi の時間成分P0が(系のエネルギー)/cに等しいように、上式で積分の前に加えた定数因子constの値を定める。
《大切な注意》
ここで、このように4次元曲面での積分によって系のエネルギーを定めるということは、系のエネルギーを集中させる特異点を排除して計算することを意味する。ラグランジアン密度Λに特異点を持たせないならば、特異点に置いた電荷の近傍の空間で場の強さが無限に大きくなり場のエネルギーが無限大になる「無限大」の問題を回避できる。電荷は(量子力学の電子の物質波のように)広がりを持った領域に分散して存在すると考え、「無限大」の問題を回避できる。
constの値は、以下の考察で求める。空間的な境界面(時間方向での凹凸がある超曲面)の各部分dSkでの体積積分は、時刻t=aでの空間的な(凹凸の無い)超平面の各部分dS0での体積積分と同じ値になる。

そして、以下の考察を続けると、constの値が定まり、系の4元運動量に対する式(32.6)が得られる。

(この積分は、3次元空間内の全ての粒子の世界線と交差する、3次元座標方向の広がりが無限大の、空間的な4次元的超曲面で微小領域dSkで体積積分する。)
テンソルTikは系のエネルギー・運動量テンソルとよばれる。
(他の方法による保存量の存在の確認)
保存量の存在の他の導出方法は、Tik =Jk という(パラメータ i 毎の)ベクトルJk の4次元発散が0であるとして、4元ベクトルJk に係る連続の方程式になっているとみなす。

つまり、Jk の時間成分J0 を電荷もどきの量とみなし、Jk の空間成分の3次元ベクトルを電荷もどきの流れとみなす。そうして、微小3次元領域に蓄積された電荷もどきが、流れ出したり流れ込んで、とにかく電荷もどきの総量が時間が変わっても保存される。そいう保存則を、その4次元発散が0になる式から把握しても良い。
(計算の見通し)
以上で導出した保存則は、ネーターの定理の手順に従って、空間と時間の一様性(並進対称性)に基づいてエネルギーの保存則と運動量の保存則とを導出したと言える。すなわち、テンソルTik の性質に空間の一様性と時間の一様性が組み込まれていると言える。ここまでの解析での大事な注意点として、未だ、空間の等方性(方向対称性)を使った保存則(角運動量の保存則)は導出していない。空間の等方性はテンソルTik の性質に組み込まれていない。エネルギー運動量テンソルTik の性質を完全に確定するためには、更に、角運動量の保存則に係る空間の等方性(方向の対称性)の条件を加える必要がある。ここまでの計算では、その条件が未だ加えられていないので解析が不十分である。32節の最後に、不足している角運動量保存則の条件が付け加えられ、それによりTik の性質が確定される。
(見通しおわり)
《対称行列を求める課題》
式(32.3)で求めたテンソルTik は対称行列ではなかった。式(32.6)の結果を変えずにテンソルTik を対称行列に変換する考え方が、32節の最後で、角運動量の保存則を導入する方法で記載されている。その前に、ここで、ちょっと寄り道をして、対称行列であらわされるエネルギー・運動量テンソルを、先に見つけておこう。
《粒子系のエネルギー運動量テンソル》
先ず、式(32.4)の意味を、以下のようにある密度で分布する粒子系に適用して考察する。ラグランジュ方程式(32.2)と、それから得られた方程式(32.4)は、一般座標qを場の一般座標だけでなく、座標の一般座標に係るラグランジアンも含めて記述されると解釈する。そう解釈すると、ラグランジュ方程式(32.2)は、場の方程式であるだけでなく、粒子系の方程式でもあると考えることができる(量子力学では粒子も場で記述されるので粒子も場の一種と考えて良いと思う)。そして、先ず、(32.4)式を、1つの i 成分に係るベクトルJk の式と考えて、以下の計算を行い粒子系のエネルギー運動量テンソルを考察する。

(この式は、3次元ベクトルである電流密度ベクトルJと、電荷の密度ρとであらわす、電荷の保存の法則の式に対応する。ただし、電荷の場合とは異なり、運動する「質量の密度ρの連続体」では、質量が運動によってγ倍になる(電荷は運動しても増えない)ので、μ≡ργという記号を導入して、この式をあらわした)。

すなわち、式(32.4)はJ0に対応する量μの体積積分が保存することをあらわしている。
《以上の式の前提条件に注意すること》
以上の式では、静止した物体の質量と運動物体の質量(γ倍)が異なることが組み込まれているので、粒子の数が保存されると仮定することとの矛盾がある。粒子の数も保存されると仮定すると、以下の問題を生じる。運動していた粒子の運動質量が静止質量よりも余分な質量を持っていた。粒子が静止したときにその余分な質量の行き場を失わないために、何等かのメカニズムか必要である。その粒子が静止するためには、その粒子の余分な質量を他の粒子の運動に転化させる、粒子同士の衝突が必要だと考えなければならない。
(エネルギー密度と運動量密度)
質量が連続した密度分布を持つと考える。質量の密度というのは,相対論的に言えば「エネルギー密度」である。また同時に,単位体積あたりに存在する運動量「運動量密度」という概念も導入する。
運動する「密度ρの連続体」のエネルギー密度は、運動によって質量がγ倍になるので、(静止系の観測者の)私にはγρc2に見えている。さて,本当にそれだけでいいだろうか。ローレンツ短縮により,連続体は進行方向に対して縮んでいるように(静止系の)私には見える。体積が縮んだ分だけ単位体積あたりの密度はγ倍に増加しているように見えるはずなのだ。よってエネルギー密度εは,γ2ρc2に見えているとするのが正解である。同様の理由で運動量密度πもγ2 ρvと表されることになる。これらを 4 元速度ui で表せば、以下のようになる。

これを美しくまとめて表現するために次のような対称行列を作ってやろう。

この対称テンソルTik を粒子の系のエネルギー・運動量テンソルと呼ぶ。
(ただし、上記のテンソルTik の式は、粒子系の流体の膨張する圧力が十分に小さく0とみなせる場合の式である。また、粒子系の流体の粘性も十分に小さく0とみなせる場合の式である。32節の主題からは外れるかもしれないが、運動する粒子系の集合(流体)には、巨視的な流体速度が現れる他に、膨張の圧力や流体の運動の粘性という、想定外の巨視的な物理量が生まれる。物理には、そういう想定外の面白さがある。)
こうして、粒子系のエネルギー・運動量テンソルが対称テンソルであることがわかった。そのため、それと対になる電磁場などの場のエネルギー・運動量テンソルも対称テンソルにならなければならないことが分かる。
なお、「粒子の系のエネルギー・運動量テンソル」は、「場の古典論」33節で初めて導入される。しかし、その導入の際に、定義無しでμ≡ργという記号をいきなり用いて、導入している。

その式が理解できずに挫折する学生も多いのではないかと思う。「場の古典論」は、数式の根底の記号の定義があいまいである、又は、定義がされていない、という致命的な欠陥があるのではないかと思う。
《場のエネルギー運動量テンソルの解析の再開》
このように、対称テンソルであらわした粒子の系のエネルギー・運動量テンソルTは、比較的簡単な考察によって求められた。その結果から、電磁場のエネルギー・運動量テンソルも対称テンソルであるらしいことがわかった。しかし、粒子系の流体のエネルギー・運動量テンソルTとして対称テンソルの式を求めたが、そのテンソルTは、定義の自由度のうちの1つの解にすぎないと考える。すなわち、そのテンソルTが必ず対称テンソルになると保証されたわけではないと考える。そのため、以下の、物理法則の本質の考察によって、式(32.3)を糸口にして、エネルギー・運動量テンソルTが対称テンソルであることを導き出す。それにより、33節で電磁場のエネルギー・運動量テンソルを導出する準備をする。
テンソルTik をラグランジアン密度Λで定義する式(32.3)は一般的にいって対称なテンソルTik をあらわしていない。特に、物理系が角運動量Mを持つならば、Tik は非対称になる。
以下では、4次元発散の式(32.4)を満足するテンソルTik の定義が一義的でなく定義の自由度を持つことを示す。次に、その自由度を持つテンソルTから、テンソルTに係る全ての性質が完備されたテンソルTを作る。そして、完備されたテンソルTは対称なテンソルであることを示す。
《テンソルφikmを微分した項の追加》
式(32.3)で定義されるTik に対して、添え字kmに関して反対称なテンソルφikmに係る項を加えて以下の式(32.7)で表したテンソルも、式(32.4)を満足する。

すなわち、以下のように、反対象テンソルと対称テンソルの積の和を計算すると、

となるからである。
式(32.6)の4元運動量Pi を求める積分は、3次元空間内の全ての粒子の世界線と交差する、x座標方向とy座標方向とz座標方向では無限遠までの広がりがある、空間的な4次元的超曲面の微小領域dSkで(標準的には平坦な領域dS0で)体積積分するものである。

その式(32.6)に、式(32.7)の、テンソルφikmをxmで微分した項を加えた場合を考える。その項を、無限遠までの広がりがx座標方向と、y座標方向と、z座標方向にある空間的な4次元的超曲面(微小領域dSk≒dS0)で3次元体積積分する。その3次元体積積分は、以下の計算のように、超曲面のx座標かy座標かz座標かが無限遠の位置の超境界線(2次元面)での2次元面積積分に変換される。(詳しくは、ここをクリックした先の6節で説明しているように、4次元的超曲面(3次元体積)の、x座標方向の端の位置や、y座標方向の端の位置や、z座標軸方向の端の超境界線の位置での2次元面での超線積分(2次元面積分)に変換される。)

以上の計算では、x1 が無限大の位置でφikm=Akm の値が0になることを使った。

上図のように、x座標の±∞の位置での超線積分(2次元面積分)になることが重要な意味を持つ。微分形式の機械的な式変形によって超面積積分が超線積分になるという公式を表面的な理解だけで覚えているだけでは、この超線積分をx座標のどの値の位置で行うかの(x=±∞で行う)、具体的な超線積分の領域の位置の認識が抜け落ちるかもしれないと思う。

以上の計算では、x2 が無限大の位置でφikm=Akm の値が0になることを使った。

以上の計算では、x3 が無限大の位置でφikm=Akm の値が0になることを使った。
以上の計算での、x座標方向とy座標方向とz座標方向では無限遠までの広がりがある空間的な4次元的超曲面(微小領域dSk≒dS0)の領域での体積積分は、x座標かy座標かz座標かが無限遠の位置の境界面での面積積分に変換される。その無限遠の位置には場も粒子もないから、この積分の値は0になる。

こうして、空間的な平坦な積分領域dS0 で計算したテンソルφの偏微分の追加項の積分の値は0になる。
また、平坦な積分領域dS0 以外の、4次元空間内で凹凸のある空間的な超曲面は、その超曲面が微小な積分領域dSi 同士を、境界を重ね合わせて形成できる。その境界で重ね合わせた両dSi の、その境界での積分の値は正負が逆になる。そのため重ね合わせた境界での積分の値が相殺される。そして、境界で重ね合わせて連結した積分領域の露出する境界の積分値のみが残る。そのため、空間的な超曲面に4次元空間内での凹凸があっても平坦な積分領域と同じく、超曲面での超面積積分(体積積分)が境界積分(面積積分)に変換される関係があると考えられる。
実際、そのようになっているかどうかを、以下の、(dx0)Λ(dx1) 面に垂直な3つの超平面を境界bと境界cで連結した超曲面を例にして、具体的に計算して確認する(ここをクリックした先の6節の説明にて、より詳しく説明している)。
先ず、左端の境界aから境界bまでの部分を計算する。
 k,m=0,2の部分も以下のように計算できる。
k,m=0,2の部分も以下のように計算できる。 
また、k,m=0,3の部分も以下のように計算できる。

次に、境界bから境界cまでの部分を計算する。

k,m=1,2の部分も以下のように計算できる。

k,m=1,3の部分も以下のように計算できる。

次に、境界cから右端の境界dまでの部分を計算する。

この計算だけで無く、k,m=0,2の部分も計算し、k,m=0,3の部分も計算するが、その説明は省略する。
以上の3つの部分を合わせた、空間的な4次元的超曲面での積分の結果は以下の式にまとまる。(なお、積分の要素のdSk は、超曲面に存在する部分のdSk のみである)。

ここで、テンソルAkm が反対称テンソルなので、以下の関係が成り立つ。

そのため、先の計算の続きは以下のようになる。

以上の計算では、相殺されずに残った境界積分は全て、x1 やx2 やx3が±無限大の位置でのφikm=Akm の値(0になる)を使うので0になった。 こうして、dS0 以外の向きの面成分も持った凹凸のある超曲面で積分しても、テンソルφの偏微分の追加項の積分の値は0になる。
(補足)
この、凹凸のある超曲面での反対称テンソルAik に係る積分は、以下の図のように解釈できると考える(そういうふうには考えにくければ、私のこの意見は無視してかまわない)。以下の図で、電気力線が凹凸のある超曲面上で表わされると解釈する。すなわち、「力線の源断面」と超曲面との交線が電気力線であると解釈するのである。そして、凹凸のある超曲面上での電場ベクトルのdivの体積積分と、その超曲面の境界を横切る電気力線の本数の積分との関係が以上の計算で扱われたと解釈する。

(補足おわり)
こうして、dS0 以外の向きの面成分も持った凹凸のある超曲面で積分しても、テンソルφの偏微分の追加項の積分の値は0になる。したがって、空間的な4次元的超曲面での積分の式(32.6)であらわされる4元運動量は、テンソルφの偏微分の追加項を加えた式(32.7)のテンソルTに替えても変わらない、一義的に定まった量なのである。
テンソルφの偏微分の追加項が加えられるので、テンソルTik の定義には式(32.7)の形の自由度があることがわかった。次に、そのテンソルTik が対称テンソルになる必然性を以下で示す。系の角運動量の4元テンソルが4元運動量によって表わすことができるという要求を使ってテンソルTik を調整すると、以下の計算によって必然的に、テンソルTik が対称テンソルになる。この要求を加える意味は、空間の方向の等方性の条件をテンソルTik を表す式に取り込み、その式があらわすテンソルTik の性質を完備させるという意味を持つ。
《角運動量テンソルの保存》
先ず、系の角運動量テンソルを以下の式(32.8)で表せるものとする条件を加える。

ここで、以下の条件式(32.9)を加える。その理由は、そうすれば、式(32.8)で定義した角運動量テンソルMik が、以下の計算の通りに、保存される(時間が変わっても変わらない)結果が得られるからである。

この条件の下で、ネーターの定理の手順に従って、以下の積分領域(空間的には無限大の広がりがあり、時間的にはt=aからbまで)で4次元体積の積分を行う。

ガウスの発散定理により以下の式が成り立つ。

0=右辺の式から、以下の結果が得られる。先ずは、空間的に無限遠方では、場が存在しないので、Tkn が0になるものとする。

すなわち、角運動量テンソルMik が保存される(時間が変わっても変わらない)結果が得られた。
このあと少し考察すれば、角運動量テンソルMik を保存するために導入した式(32.9)の条件を満たすテンソルTik は対称テンソルになることが導き出せる。そのため、エネルギー運動量テンソルTik は必然的に対称テンソルになる。
Tik が対称テンソルになる結論は、場のエネルギー運動量テンソルTik に限定されない。式(32.1)のラグランジアン密度を粒子系のラグランジアン密度であると解釈すれば、式(32.3)は一般座標の関数の粒子の密度分布を持つ粒子系(流体)のエネルギー運動量テンソルTik を表していると解釈できる。すなわち、巨視的な流体速度が現れる他に、膨張の圧力や流体の運動の粘性という、想定外の巨視的な物理量も現れている粒子系の集合(流体)のエネルギー運動量テンソルTik を表していると解釈できる。上記の考察によって、そういう粒子系でのエネルギー運動量テンソルTik も対称テンソルになる。
また、ここをクリックした先の非相対論的な力学を教える文献でも、同様なことが説明されている。「角運動量保存則は、角運動量の時間変化率がトルクの和に等しいとして表される。」とあり、その関係を利用して角運動量保存則が成り立つ場合を解析すると、応力テンソル(エネルギー運動量テンソルに対応するテンソル)が対称テンソルになることが導かれる。逆に,応力テンソルが対称であることにより,角運動量保存則が満たされることが示される。
ここをクリックした先のサイトにも、非相対論的力学で、応力テンソル(エネルギー運動量テンソルに対応するテンソル)が対称テンソルになる理由が説明されている。
ランダウの「場の古典論」だけに、この相対論的エネルギー運動量テンソルTik が、角運動量の保存則を組み込むことで対称テンソルになる理由が書かれているのではないかと思う。物理の参考書毎に、著者のオリジナルな説明があって、全てが書かれている参考書は無いのではないかと思う。全分野の物理の参考書をいくつも読んで物理知識を全力で連携していく必要があると思う。また、自分で計算して確認して自力で理解することで、物理の参考書に書かれている説明の行間を埋めていく必要があると思う。
これで、やっとのことで、次の33節で電磁場のエネルギー運動量テンソルTik を導き出す準備が整った。
(注意点)
(1)場のエネルギー運動量テンソルTが対称テンソルである条件として、場の一般座標qi である場の4元ベクトルAi の関数として記述される場のラグランジアンが、空間の方向を変えても変わらない空間の方向対称性(空間の等方性)がある条件が必要です。
(2)同様に、一般座標xi の関数の密度分布を持つ粒子系の流体のエネルギー運動量テンソルTが対称テンソルである条件として、その粒子系のラグランジアンが、空間の方向を変えても変わらない空間の方向対称性(空間の等方性)がある条件が必要です。
【リンク】
pdf 古典力学 (解析力学)
東京大学数理物理学班「古典力学」
「高校物理の目次」
ランダウ「場の古典論《6節後段》」テンソル解析の公式集
▷4元グラジエント
▷(1)4次元空間のなかの曲線のうえの積分
▷(2)4次元空間のなかの(2次元)曲面のうえの積分
▷相対論の4次元空間(ミンコフスキー空間)でのホッジの星印作用素の定義
▷(3)4次元空間のなかの超曲面、すなわち、3次元多様体のうえの積分
▷(4)4次元の体積にわたる積分
▷微分形式
▷4次元座標の連続関数に関するガウスの発散定理
▷4次元座標での3次元超曲面での積分を、超曲面を包む2次元面での積分に変換する定理
▷ランダウの「対偶」の定義の修正
【場の古典論】
【第1章】相対性原理
《第6節後段》21p~24p テンソル解析の公式集
この部分を以下で解説するが、このページの最後に記載した、《ランダウの「対偶」の定義の修正》を最初から行って、説明を進めた方が説明がスッキリするので、以下の説明の早い時期に、その定義を修正して説明するようにした。
〔§6でのテンソル解析の公式集を理解する基礎知識として《微分形式》を学んでおいた方が良いと思う〕
『これから,今まで知っていた代数と少し異なる新しい代数を勉強します.代数とは,乗法の定義されたベクトル空間のことでしたが,これから考える乗法は,既にご存知のベクトルの外積に少し似た乗法です.これを 外積代数 と呼びます.しかし,これから考える乗法はベクトルの外積よりも,もっと一般的なものですので,ひとまずベクトルのことは忘れておくと良いと思います.外積代数はそれ自体でも面白いのですが,微分形式もしくは外微分形式と呼ばれる強力なツールを勉強するための土台になります.(微分形式は,物理や工学などに幅広く応用できる強力な理論です.外積代数だけでは,少し数学的すぎて無味乾燥に感じるかも知れません.)どうしても微分形式を早く勉強したい人は,外積代数カテゴリーの後半の記事は飛ばして先に行っても大丈夫ですが,最低 ホッジ作用素 の記事の内容は押さえておいた方が良いと思います.』
《ポアンカレの補題》任意の次数の微分形式に対し,二回外微分を取ったら零になります.
また、この微分形式の説明を理解する基礎知識として「テンソルの概念の初歩」を学んでおくと良いと思います。
『外積のルール 1 と 2 を持った算法の構造を,外積代数と呼びます.外積代数では,外積の計算を一般の次元でも使えるように少し拡張したウェッジ積という乗法を考えます.』
4次元テンソル解析の微分および積分演算の公式を述べる。
《4元グラジエント》
ローレンツ変換によって各世界点での値が不変なスカラー量である4次元座標に対する連続関数φの4元グラジエントは(共変型の)4元ベクトルである。

実際、スカラーφの微分量dφはスカラーであるが、この量は以下の式のように、この4元グラジエント∂φと(反変型の)4元ベクトルdxi の積であらわされる。そのため、この4元グラジエント∂φが(共変型の)ベクトルであることが確かめられる。

微分演算子∂i は(共変型の)ベクトルとみなせる。そのため、以下の式のような、この演算子∂i と(反変型の)4元ベクトルAi との積はスカラーになる。

《4次元空間での積分の形》
3次元空間では積分は、体積、面積、線分で行なうことができる。4次元空間では、以下の4つの型の積分が可能である。
《(1)4次元空間のなかの曲線のうえの積分》
積分要素は弧長の要素である動径4元ベクトルdxi である。
《(2)4次元空間のなかの(2次元)曲面のうえの積分》
3次元空間のなかの(2次元)曲面のうえの微小面積要素のXY平面への射影の面積ΔSxyは下図のようになる。


そして、3次元空間での立体的な微小面積要素は、3つの座標平面への射影の面積を成分とする3次元のベクトル(ΔSyz,ΔSzx,ΔSxy)=dSm であらわされる。
4次元空間のなかの(2次元)曲面のうえの微小面積要素dfik も、4次元空間での6つの座標平面への射影の面積(6つ)を成分とする6次元のベクトルであらわされる。(2つの基底の組合せ(ei)⊗(ek)であらわす面要素も、ベクトル空間の基底であり、その組合せ基底(ei)⊗(ek)の数がそのベクトル空間の次元である)。第1のベクトルと第2のベクトルの張る面積の、6つの座標平面への射影は以下のように計算できる。例えば、1つの面要素をあらわす複合基底(e1)⊗(e2)の係数は、以下の式で計算できる。単独基底(e1)と(e2)を基底とする第1のベクトルと第2のベクトルをウェッジ積Λで掛け合わせると複合基底(e1)⊗(e2)を基底とする(面をあらわす)ベクトルになる。基底が複合基底であるベクトルをテンソルと呼ぶ。第1と第2のベクトルの順番を逆にしたウェッジ積の符号は逆になる。このように、2つのベクトルのウェッジ積で与えるテンソルは反対称テンソルである。

任意の方向を向いた2つのベクトルのウェッジ積を計算すると、速やかに、6つの座標平面への射影の6つの複合基底(ei)⊗(ek)と係数dfik の積の和であらわすことができる。微小面積要素dfik は反対称テンソルである。なお、ベクトルで注意すべきことは、ベクトルは、基底ei ((ei)⊗(ek)という複合基底を持つベクトルはテンソルと呼ばれる)と係数xi (またはfik )とのセットだということです。
《第1のポイント》
先ず、以下の擬テンソルεについて、添字の上げ下げはテンソルと同様にできる。そのため、以下の式の関係が成り立っている。

《第2のポイント》
次に、ホッジの星印作用素*(定義に注意)に関する以下の式が成り立っている。

また、以下の式の関係が成り立っている。

(注意)なお、ホッジの星印作用素を2重に作用させた場合に、以下の例のように、元の要素の符号が変わってしまい元に戻らない場合がある(いつもそうであるとは限らない)ことに注意。

ランダウの式6.12の記述には、どの項が星印作用素であるかが明示されてない(ホッジの星印作用素の場合は、どの項が星印作用素であるかによって式の符号が逆になる)あいまいさがある。§6の文脈の示唆から式を解釈すると、式6.12は、下記の(6.12)のように星印作用素の項を持った式であると解釈される。

式6.12は、星印作用素との関係があいまいな式である。また、ホッジ双対の写像関係の正しい定義は、同じ上付き記号の微分のウェッジ積であらわした基底の間の関係であるが、ランダウの「対偶」の定義では、ホッジの星印作用素の項の添え字の上付きと下付きを逆に表現していることに注意すべきである。そして、更に式の符号が逆に定義されていると考えられる。
以降の説明をスッキリさせるため、この際に、式6.12の表現を明確に定義する。

このランダウ「対偶」の定義は、以下の定義だと考えるとわかりやすいと思う。

問題を簡単化するために、再度、3次元空間に戻って考える。

3次元空間では、この反対称テンソルdfik のかわりに、以下のように、この反対称テンソルdfik の対偶(ホッジ双対 Hodge)の3次元ベクトルdSm を、エディントンのイプシロンεmik を使って計算して、その対偶(ホッジ双対)ベクトルdSm に微小面積要素を代表させている。

これは、面積要素の法線方向を持つベクトルである。そして、ベクトルdSm の絶対値がこの微小面積要素の面積に等しい。
4次元空間では、テンソルdfik に対してはそういう法線ベクトルを作ることはできないが、4次元用のエディントンのイプシロンεmpik を使って計算して、そのテンソルdfik の対偶(ホッジ双対の定義とは左辺の星印作用素の項の添え字の上下が逆ではあるが)テンソルdf*mp を作ることはできる。


この対偶テンソルdf*mp は、2次形式から 2次形式に写像したホッジ双対なテンソルである。
以降の説明をスッキリさせるため、この際に、誤りを正しておこうと思う。この式6.11の正しい定義は、以下の定義だと考える。

このランダウ「対偶」の定義は、以下の定義だと考えるとわかりやすいと思う。

ホッジの星印作用素の定義は「超簡単!ベクトル解析、他」(神谷幸秀:高エネルギー加速器研究機構)が参考になると思う。 「ホッジの星印作用素は、大雑把に言えば、 k 次の微分形式(の基底)とその微分形式にこの作用素を作用させたものとの外積(wedge積)をとると、最高次の微分形式になるようなものである。(ただし、計量テンソルgik の対角成分がー1になる成分の数(計量を負とする基底の数)が奇数ある場合は、それにー1を掛け算する) 」この定義に従い、星印作用素は3次の微分形式に作用させる場合も、2次の微分形式に作用させるときも、同じεmpik を使った式でなければならない。 ホッジ双対についての、九州大学(吉田茂生)の講義ノート「ベクトルとテンソル」も参考になると思う。
《微分形式の引き戻し》《ホッジの星印作用素》
(ここをクリックした先のサイトも参考になる) 「いままで3次元空間での『ベクトルの外積』として知っていた計算の正体は,『 ベクトルの外積の結果のベクトルdSi を作る元の2つのベクトルの2次元のウェッジ積d(Xk) Λd(Xm) に3次元のホッジの星印作用素を作用させて、(3-2)=1次元のウェッジ積dSiに写像したもの』だったのです.」
4次元の場合では、k個の方向で定義されるk次元の積分範囲の演算子であるk 次元の微分形式(第1の微分形式)と、そのk個の方向に垂直な(4-k)個の方向で定義される(4-k)次元の微分形式(第2の微分形式)をウェッジ積Λで結んだ最高次(4次元)の積分範囲の演算子を考えて、以下のホッジの星印作用素を定義する。
ホッジ双対の写像関係の正しい定義は、同じ上付き記号の微分のウェッジ積であらわした基底の間の関係である。
その定義に従ったホッジの星印作用素*の厳密な定義の式を以下の式であらわす。(相対論の4次元の計量テンソルの4つの対角成分のうちの3つが、g11=g22=g33=-1なので、定義の式にマイナス符号が付く)。その厳密な定義の式に従ってウェッジ積Λを使った微分形式で書くと式が分かりやすくなると思う。
《相対論の4次元空間(ミンコフスキー空間)でのホッジの星印作用素の定義》
以下の関係式を成り立たせるホッジの星印作用素を定義する。

そのために、ホッジの星印作用素を以下の式で定義する。



(注意)ランダウの§6の「対偶」の定義は、ホッジの星印作用素の項の添え字の上付きと下付きを逆に表現しているので、ランダウの対偶の定義を具体的にリストアップすると、以下の関係が成り立つ。
ホッジの星印作用素を2重に作用させた場合に、元の要素の符号が変わってしまい元に戻らない場合がある。ランダウが§6で定義する「対偶」(定義を正しく修正したもの)でも、2重に作用させた場合に元に戻らない場合がある。
《以下は、ランダウの「対偶」の演算のリストである》

微小面積要素をあらわすテンソルの6つの基底が6次元ベクトルを構成する。ホッジ双対(Hodge)(対偶)な面積要素df*mp のベクトルは、面積要素dfik の6次元ベクトルに垂直な6次元ベクトルであらわされる。 この微小面積要素のホッジ双対(対偶)への変換操作は、1つの選択肢としては、以下の座標変換を行なうことによって実現できる。

この座標変換を対偶の具体的変換として行なうならば、全てのベクトルが、それに垂直なベクトルに変換される。 微小面積要素の対偶の要素を作る具体的座標変換の選択肢がその他にも種々考えられるが、いずれの座標変換でも、全てのベクトルが、それに垂直なベクトルに変換されると思う。
対偶(ホッジ双対)を作る座標変換にどの選択肢を選ぶ場合でも、面要素dfik 上の線分の方向は、その面要素のホッジ双対な面要素df*mp 上の線分に垂直であることを、以下で考察する。先ず、(X,Y,Z,W)の4次元における面要素の方向は、XY平面、XZ平面、YZ平面、XW平面、YW平面、ZW平面との6つがあるので、面要素の方向をあらわす反対称テンソルdfik の成分の集合は6次元ベクトルであらわされる。元の面要素dfik が6次元ベクトルの1つの成分のみであらわされるように、その面要素がX軸とY軸が張るXY平面に平行になるようにXYZW座標軸を定めてベクトルの基底(基底とする面要素の方向)を対角化する。

XY平面に平行な面要素dfxy のホッジ双対な面要素df*mp が、エディントンのイプシロンεmpik を使ってあらわされると、その面要素df*mk はX軸にもY軸にも垂直な2つの軸のZ軸とW軸の張るZW平面に平行な面要素df*zw になる。(XY平面に平行な面要素dfxy に垂直な5つの平面の、XZ平面、YZ平面、XW平面、YW平面、ZW平面、のうちの1つのみが選ばれる)。
(1)面要素dfxy と面要素df*zw は互いに垂直であるため、面要素dfik をあらわす(6つの平面を成分とする)6次元ベクトルと、ホッジ双対な面要素df*mk をあらわす6次元ベクトルの内積は0になる。
(2)しかも、それだけでは無く、面要素dfik を張るXY軸のいずれにも垂直な軸がホッジ双対な要素の軸として選ばれる。3次元空間では、それはZ軸1つだけであったが、4次元空間では、それにはZ軸とW軸との2つの軸がある。その2つの軸で張るZW平面が、ホッジ双対な面要素df*mk の面になる。そのように、ホッジ双対では、元の面要素のうえのどの線分にも垂直(それが含む全ての線分が垂直)な軸で構成される面要素df*mk を選ぶのである。
実際、以下の計算によって、面要素のテンソル(6次元ベクトル)同士の内積を計算すると値が0になる。
ここで、以下の、反対称テンソルと対称テンソルの積が0になる公式を利用して計算する。

この公式を使って、以下で、面要素のテンソル(6次元ベクトル)同士の内積を計算する。

このように、内積の値が0になる。内積が0になるため、元の面要素dfik と、ホッジ双対な面要素df*mk が、少なくとも互いに垂直であることがわかる。しかも、それだけでは無く、面要素dfik のうえのどの線分も、ホッジ双対な面要素のうえの任意の線分に垂直になる。
ちなみに、平行四辺形の面要素dfik の面積は、その面要素を張る2つのベクトルの長さの積と、その2つのベクトルの間の角度θの正弦 sinθとの積であらわされる。それ以外のその面積の計算方法としては、以下のように、面要素dfik 同士の内積でも計算できる。ただし、その内積は、法線が表面側と裏面側の面を数えるので面積が2重に足される計算になるので、面要素dfik の面積の2乗の2倍になることに注意する必要がある。

以上の計算の最後の段階での、4元ベクトルdrの2乗や4元ベクトルduの2乗の項は、相対論的4次元空間における共変型4元ベクトルと反変型4元ベクトルの内積としてのベクトルの2乗(ローレンツ変換によって変わらない不変量)をあらわしていると解釈して欲しい。すなわち、以上の計算は、4元ベクトルdrと4元ベクトルduの張る微小面積要素の相対論的な2乗の値としての(ローレンツ変換によって変わらない)スカラー値を計算している。
《(3)4次元空間のなかの超曲面、すなわち、3次元多様体のうえの積分》
3次元空間でも、4次元空間でも、3つのベクトルの張る平行6面体の体積は、2つのベクトルの張る面積に、その面に垂直方向の、3つ目のベクトルの高さの積で与えられる。3次元空間では、その体積は、3つの3次元ベクトルの成分から作られる3行3列の行列式に等しい。(行列式の値は正にも負にもなり得ることに注意)。4次元空間では、超曲面に平行で互いに直交する3つの基底ベクトルXk ,Xm ,Xp への、微小体積要素を張る3つのベクトルからの射影(1つのベクトル毎に3つの基底への射影の3つの成分)を求める。そして、その射影の成分から作られる3行3列の行列式が微小体積要素の体積をあらわす。3つの基底ベクトルを基準にした体積(超面積)なので、その行列式の体積をdSkmp というテンソルであらわす。特に超曲面上の積分要素としては、テンソルdSkmp にホッジ双対な4元ベクトルdSi を使うのが便利である。
以下で4元ベクトルdSi を計算する。dSi はランダウの表現を用い、ホッジの星形作用素の添え字の上付きと下付きを逆に表現する。6節の式6.12の定義は正しく修正した定義に従う。


ここで、dSkmp は、k方向の4元ベクトルとm方向の4元ベクトルとp方向の4元ベクトルの張る各方向に作用する体積を行列式であらわすので、添え字k,m,pを入れ替えると体積の値の正負が逆転する。そういうクセのあるものを積分の演算子として使う。そのdSkmp という積分の演算子を、各方向毎の積分の演算子をウェッジ積Λでつないであらわした3方向での積分の演算子であらわすことにする。dSkmp の持つ、添え字の入れ替えで正負が逆転する性質、と同じ性質を持たせるために、ウェッジ積でつないだ演算子の列d(xk) Λd(xm) Λd(xp) は、積の順序を入れ替えるとマイナス符号が付く。

微小体積要素のテンソルdSkmp にホッジ双対な4元ベクトルdSi の方向は、微小体積要素の積分の各演算子のあらわす積分方向のk軸m軸p軸の各方向に垂直である。積分演算のテンソルdSkmp の面上の全ての直線の方向は、i 軸に垂直である。
ここで、基準軸i ,軸k ,軸m ,軸p であらわした超曲面のテンソル及び4元ベクトルの成分を、基準軸WXYZ軸でのテンソル成分およびベクトル成分に書き直して考える。そのように基準軸を変えて書き直したテンソルの成分と4元ベクトルの成分の間でも上の式(6.12)が成り立つ。基準軸の変更によって4元ベクトルdSi はW軸X軸Y軸Z軸へ射影した成分のdS0 ,dS1 ,dS2 ,dS3 であらわされる。超平面の微小超面積要素をあらわすテンソルの成分も、その微小超面積要素のXYZ超平面への射影、WXY超平面への射影、WYZ超平面への射影、WZX超平面への射影の成分に書き直される。それらのWXYZ軸を基準にした4元ベクトルやテンソルの成分は、以下のようにあらわされる。

幾何学的には、この4元ベクトルdSi の絶対値は超曲面要素の"面積"に等しく、方向はこの超曲面要素を張る3つの座標軸に垂直な法線方向に一致する。dS0=dxdydzは、明らかにX軸とY軸とZ軸が張る超平面の法線方向のW軸(ct軸)への、4元ベクトルdSi の射影に等しい。
《相対論的4元ベクトルが問題を難しくしている》
相対論的4元ベクトルが4次元ベクトルとテンソルの計算を難しくしていることを注意しておく。相対論的な4元ベクトルとテンソルの扱いは、単純な4次元空間のベクトルおよびテンソルと扱いが異なる。先ず、ベクトルの長さの2乗の計算が異なる。しかしながら、両者とも同じく、微小体積要素をあらわすテンソルdSkmp は反対称テンソルである。

《(4)4次元の体積にわたる積分》
積分要素は4次元体積要素である。

この要素の値はローレンツ変換によって変わらないスカラーである。4次元空間のある部分の体積は、座標軸の回転変換およびローレンツ変換(これも広い意味での座標軸の回転変換の一種である)に対して不変である。
ただし、詳しくは、下図のように、4次元空間で4つの4元ベクトルri ,uk ,bm ,hp が張る微小体積は、以下の式のように、反対称テンソルのエディントンのイプシロンを使った4行4列の行列式で体積の値が計算される。その微小体積の値は座標の置き換えによって値が変る偽スカラーである。

《微分形式の目次》《微分形式》 《多様体上の1次微分形式》《多様体上の微分形式とその外微分》《微分形式のいくつかの性質》《境界付き多様体とStokesの定理》
(ここをクリックした先のサイトも参考になる)
ここで、積分のための座標の微小量dX0 =cdtや、dX1 =dxやdX2=dyやdX3 =dzを、微小な積分の体積部分dSkmp が行列式であらわされることに対応させ、微小体積部分の各方向のベクトルに対応する積分の演算子にする。異なる座標の方向のこれらの積分の演算子を外積で組み合わせた複数次元での積分演算子を作る。すなわちdSkmp に対応する複数次元での積分演算子を、各座標方向の積分演算子をくさび積Λ(wedge積)で結んだ微分形式であらわす。

そのくさび積の演算子の列(微分形式)があらわす微小な複数次元の面積(あるいは体積)は、正の数で把握される積分範囲の微小面積に対する比が±1になる。くさび積があらわす微小面積の値が、積分の正の値の微小領域に対する比が1であったり、(-1)であったりする。その面積の値の比が±1で変動するのを打ち消すように値が正と負になるように微分形式の値を定める。そうすると、以下の関係がある。

《4次元座標の連続関数に関するガウスの発散定理》
3次元空間でのガウスの発散定理は以下の式の定理であった。


左右の辺を移項して書くと以下の式であらわせる。

体積を包む閉じた曲面のうえの積分を、積分要素dSi を以下の演算子でおきかえることによって、その曲面に包まれる体積についての積分に転換する定理である。

この定理を参考にして、それを4次元空間に拡張した積分を以下のように計算する。先ず、微小超曲面のウェッジ積にホッジ双対な4元ベクトルdSi の方向を、4次元体積の領域を包む4次元超曲面の外側に向けて積分する。また、ウェッジ積が積分要素の積の順序の入れ替えによって値の符号を変える反対称テンソルであること、4次元体積要素をあらわすウェッジ積の符号に注意しつつ計算する。


以上の計算をまとめると、以下の結論になる。

このように、4次元の体積を包む閉じた超曲面のうえの積分を、積分要素dSi を以下の演算子でおきかえることによって、その超曲面に包まれる4次元体積についての積分に転換できる。

ここでの4次元の体積での積分は、5次元以上の空間内で凹凸がある4次元空間を体積積分しているわけではない。凹凸が無い平坦な4次元空間での体積積分である。そのため、次に説明する4次元空間内で凹凸のある超曲面での積分の場合とは異なり、例えば32節で4次元空間でテンソルを積分する場合へ定理を適用する場合であっても、そのテンソルが反対称テンソルに限定されるという制約も無い。この定理は、反対称テンソルの使用に限定される微分形式の定理よりも緩い条件で適用できる定理である。
《4次元座標での3次元超曲面での積分を、超曲面を包む2次元面での積分に変換する定理》

式6.17に係る定理で用いるホッジ星印作用素*は以下のように定義される。

以下の計算によって、反対称テンソルAik に関する式6.17の定理を導き出す。ただし、式6.11の「対偶」の元の定義使うと、式6.17とは符号が異なる解が得られる。式6.17が符号が異ならずに成り立つために、式6.11の「対偶」の定義を修正した定義を使って計算する。

すなわち、x1方向の境界点を含む(dx2)(dx3)面で境界積分する。
(注意)この式の最後の行では、4次元超曲面(3次元体積)dS0 を包む2次元面df*01 での積分の式という積分の形になる。その積分は、4次元超曲面(3次元体積)dS0 を包む全ての面での積分では無い。X1方向に垂直な面の面の方向での2次元面df*01 の面(dX2, dX3の張る面=dX0 に垂直、かつ、dX1 に垂直な面)の方向だけで包む2次元面での積分である。

すなわち、x0 軸方向に垂直である4次元超曲面d(S0) の全表面のうちの一部だけを包む(d(X1),d(X2) の張る面の側は包まず、d(X1),d(X3)の張る面の側も包まない)2次元面での積分をあらわしている。(参考ページが、ここをクリックした先にある)4次元的超曲面(3次元体積)での積分を、その4次元的超曲面(3次元体積)の端の超境界線(2次元面)での超線積分(2次元面積分)に変換する境界の位置の具体例がここをクリックした先にある。

すなわち、x2方向の境界点を含む(dx3)(dx1)面で境界積分する。

すなわち、x3方向の境界点を含む(dx1)(dx2)面で境界積分する。
以上の3つをまとめると、反対称テンソルAik に関するdS0による積分の公式(h=0の場合の、以下で与える公式(1)および公式(2))になる。その公式は、ベクトルA0kに関する3次元空間でのガウスの発散定理と同じ定理になる。この公式を理解するためには、ホッジの星印作用素の式を含む一連の式は無くても良い。
例えば、以下のように公式を把握した方が良い。

次の場合の積分の計算を続ける。

すなわち、x2方向の境界点を含む(dx0)(dx3)面で境界積分する。

すなわち、x3方向の境界点を含む(dx2)(dx0)面で境界積分する。

すなわち、x3方向の境界点を含む(dx0)(dx1)面で境界積分する。
以上の計算をまとめると、h=0,1,2,3 の4つのhの1つずつに成り立つ以下の各式(hを1つの値に固定した1つ式が、hの値に応じて4つある)であらわされる公式が成り立つ。

(注意はじめ)
この最後の式では、公式(1)と公式(2)との2つの積分の右辺の和を2で割った公式にした。df*kh という面積分は、k方向とh方向とに垂直な他の2つの方向のベクトルが張る面で積分する。その積分面は、d(Sh) という超曲面に垂直な2次元面であって、更に、その超曲面内から超曲面の境界を横断するk方向にも垂直な2次元面であって、かつ、超曲面の、任意のk方向の端の境界点を含む2次元面で積分することを意味する。任意のk方向の端の境界点の集合が超曲面を包み、積分面を構成する。
(注意おわり)
上の(hの値に応じた)4つの式の和をとれば(全てのhの値で和をとった)以下の式が成り立ちはするが、以下の式よりも、hの値に応じた上記の4つの公式の1つ1つに分けた公式を把握する方が望ましいと考える。

そうする方がdf*hk での面積積分の具体的積分範囲が明確に定義されるので、計算の見通しが良いからである。
《凹凸のある超曲面での積分の定理に拡張》
また、4次元空間内で凹凸のある超曲面が、微小な積分領域dSi 同士を境界を重ね合わせて形成できる。その境界でつないだ両dSi の、その境界での境界積分の値は正負が逆になる。そのため重ね合わせた境界での積分の値は相殺される。そして、境界で重ね合わせて連結した積分領域の露出する境界での境界積分のみが残る。そのため、超曲面に4次元空間内での凹凸があっても平坦な積分領域と同じく、超曲面での超面積積分(体積積分)が境界積分(面積積分)に変換される関係があると考えられる。
実際、そのようになっているかどうかを、以下の、(dx0)Λ(dx1) 面に垂直な3つの超平面を境界bと境界cで連結して構成した超曲面を例にして、具体的に計算して確認する。

このうち、境界bで接続する2つの部分を具体的にあらわす。境界aから境界bまでの部分(dS0 のみがある)は以下の形である。

境界bから境界cまでの部分(dS1 のみがある)は以下の形である。

境界bは境界面ABCDである。この境界面ABCDを重ねて、上図のabの部分がx1 方向で接続し、bcの部分がx0 方向で接続することがわかる。境界面ABCDは、ab部分直方体の外側を向いた左回りの表面であり、bc部分直方体の内側を向いた左回りの境界面であることが分かる。そのため、境界面ABCDに対してab部分とbc部分が互いに反対側で接続していることがわかる。
先ず、左端の境界aから境界bまでの部分を計算する。

k,m=0,2の部分も以下のように計算できる。

また、k,m=0,3の部分も以下のように計算できる。

次に、境界bから境界cまでの部分を計算する。

k,m=1,2の部分も以下のように計算できる。

k,m=1,3の部分も以下のように計算できる。

次に、境界cから右端の境界dまでの部分を計算する。

この計算だけで無く、k,m=0,2の部分も計算し、k,m=0,3の部分も計算するが、その説明は省略する。
以上の3つの部分を合わせた、4次元的空間内で凹凸のある超曲面での積分の結果は以下の式にまとまる。(なお、積分の要素のdSk は、超曲面に存在する部分のdSk のみである)。

ここで、テンソルAkm が反対称テンソルなので、以下の関係が成り立つ。

そのため、以下の関係が成り立つ。

以上の計算では、境界での積分は、境界bと境界cが相殺されて消え、残った境界のみの積分になった。 こうして、超曲面に4次元空間内での凹凸がある場合も平坦な積分領域での計算と同じく、超曲面での超面積積分(体積積分)が境界積分(面積積分)に変換される関係がある。
この関係が成り立つのは、テンソルAkm が反対称テンソルであるからである。テンソルAkm が対称テンソルの場合はこれは成り立たない。超曲面に4次元空間内での凹凸がある場合には、テンソルAkm が反対称テンソルであることがこの公式の必須条件である。具体例で考えたことで、この条件の必然性がハッキリ分かった。こういう公式の意味がハッキリわかるので、公式を具体例で確かめるということは止められないと思う。
この公式は、以下の微分形式であらわす定理の系である(ここで、∂Sは境界での積分をあらわす)。(ここをクリックした先のサイトが参考になる)。


(6.17)
(注意)ここで、微分形式の定理を使うためにテンソルAik が反対称テンソルであることが必要であった。4次元空間内で凹凸のある超曲面において一般的に成り立つ定理のためにAik が反対称テンソルであることが必要だったのである。しかし、4次元空間内で凹凸の無い平坦な超曲面のみでは、テンソルAik が反対称テンソルである必要が無いことに注意すべきである。その理由により、4次元空間内で凹凸のあるわけでは無い4次元体積での積分にかかわる4次元でのガウスの発散定理においては、その定理でテンソルAik を使う場合でも、そのテンソルは反対称テンソルで無くても定理が成り立つ。
(注意おわり)
以上で得た式6.17の解は式6.11の符号を変えて定義を修正しないと符号が異なってしまう。この6節の一連の公式が成り立つためには、ランダウの「対偶」の定義の式6.11とその他の式を、ホッジの星印作用素の式から符号を変えて定義する必要がある。すなわち、以下のように定義する必要がある。
《ランダウの「対偶」の定義の修正》

このランダウ「対偶」の定義は、以下の定義だと考えるとわかりやすいと思う。


このランダウ「対偶」の定義は、以下の定義だと考えるとわかりやすいと思う。

(注意)ランダウの§6の「対偶」の定義は、ホッジの星印作用素の項の添え字の上付きと下付きを逆に表現しているので、ランダウの対偶の定義を具体的にリストアップすると、以下の関係が成り立つ。
ホッジの星印作用素を2重に作用させた場合に、元の要素の符号が変わってしまい元に戻らない場合がある。ランダウが§6で定義する「対偶」(定義を正しく修正したもの)でも、2重に作用させた場合に元に戻らない場合がある。
《以下は、ランダウの「対偶」の演算のリストである》

【リンク】
「高校物理の目次」
ランダウ_場の古典論《14節 角運動量》の考察
▷角運動量4元テンソルの行列表現
▷回転粒子対アニメーション
▷速度vで運動する慣性基準系K’での角運動量
【場の古典論】
【第2章】相対論的力学
《第14節》角運動量
第14節には、ランダウ(1908-1968)の没後に書き加えられた部分の解釈が難しいので要注意と考えます。先ずは、第14節の内容を紹介し、次に、解釈の難しい部分を詳しく解析します。
《大前提》
先ず、空間が一様かつ等方的であり、時間も一様である性質を持った慣性系で記述することを大前提にして考える。
空間の等方性は、ラグランジュアンが4次元空間の回転角度にかかわる変数をあらわには含まない(循環座標)ことを意味する。閉じた系に対しては、その空間と時間の等方性のために、ラグランジュアンは4次元空間の回転によって変化しない。
xi を慣性系Kにおける粒子の、時刻t=0 における座標とする。4次元空間において、慣性系の原点のまわりに無限小回転をおこなおう。これは、座標xi と新しい座標x’i との差 x’i - xi が無限小の係数 δΩik を持つ1次式(14.1)で与えられるような変換を行うことに相当する。

ここに4元テンソル δΩik の成分は、回転のさいに、時刻t=0 における慣性系の原点と粒子の位置との間の世界間隔 ds (動径ベクトルの長さ)が変らない:

という関係を満足しなければならない。
式(1)に式(14.1)を代入する。

この式(2)は、任意のxiに対してみたされなければならない。(xi)(xk) が対称テンソルであることを考えると、δΩik は反対称テンソルでなければならない。

4次元空間の回転に係る物体の変数(パラメータ)であるδΩikはラグランジアンにあらわには含まれない(循環座標)。したがって、このパラメータに対応する一般化運動量は保存される。
作用Sを座標の関数とみなすと、「力学」の43節で説明されたように、一般化運動量pi が、作用Sの座標xi による偏微分であらわせる。 すなわち、pi=∂S/∂xi で与えられる。ここで9節の式(9.12)によるpi の定義を使う。

である。和は系の粒子全部にわたる。この式に式(14.1)を代入する。

ここで、同じものをあらわす2つのパラメータを1つで代表させる(教科書別:【pdf】「場の古典論」前半)。

4次元空間の回転に係る物体の変数(パラメータ)であるδΩikはラグランジアンにあらわには含まれない(循環座標)。したがって、このパラメータに対応する一般化運動量は保存される。
作用Sを座標の関数とみなすと、「力学」の43節で説明されたように、この一般化運動量は、作用Sの座標による偏微分であらわせる。 すなわち、この一般化運動量は∂S/∂Ωik (i<k)で与えられる。(14.3b)から、

が一般化運動量である。こうして、閉じた系では、この式の右辺のテンソルであらわされる一般化運動量が保存され、物体のテンソル
 (14.4)
(14.4) (誤植を訂正した)が保存されることがわかる。この式の各成分は、i<kの場合で定義されたが、i>kの場合でのテンソルの成分もこの式で定義することにする。この反対称テンソルを角運動量4元テンソルという。(「角運動量4元テンソルの行列」は、ここをクリックした先にある)。
このテンソルの空間成分は、明らかに、3次元角運動量

の成分

になっている。
(上記の式(14.4)の(静止系Kでの)角運動4元テンソルMは静止系Kの原点に対して計算する。下記の式(14.4b)の(慣性基準系K’での)角運動4元テンソルM’は慣性基準系K’の原点(時刻t=0では静止系Kの原点に一致する)に対して計算する。その慣性基準系K’の原点が静止系Kの原点に一致する時刻t=0で計算しても他の時刻の場合と同じ角運動量になるので、その時刻t=0に、静止系Kの原点に対して計算したとみなせる。(静止系Kの原点は静止系Kでは回転物体の重心であるが、後で説明するように、慣性基準系K’では回転物体の重心では無くなる)。)
 (14.4b)
(14.4b)成分

は、ベクトル

(誤植を訂正した)を作る。
(注意)このベクトルは、角運動量4元テンソルの成分で構成するベクトルなので4元ベクトルでは無いことに注意すること。後に23節で学ぶ電場や磁場も、電磁場テンソルの成分で構成するベクトルなので4元ベクトルでは無い。
閉じた系に対して、Mik が保存されることから、

が成り立つ。他方、全エネルギー ΣE も保存されることから、この等式を

という形に書くことができる。これから、動径ベクトル
 (14.6)
(14.6) をもつ点は速度
 (14.7)
(14.7) で一様に動くことがわかる。この速度は、系全体としての運動の速度にほかならない。(この速度は(9.8)によってその運動量とエネルギーとに関係づけられる)。式(14.6)は、系の慣性中心(重心)の相対論的な定義を与えるものである。
この式(14.6)による重心の定義は、もっと詳しく説明すると、以下の式のように、
(重心位置)=(4元ベクトルに係る量)+(角運動量4元テンソルに係る量)
で定義したことを意味する。

《数理部地理学班》解説PDF: [2]古典力学の解説PDF
相対論では、並進対称性だけでは重心の速度が全運動量に比例すること(上式の(14.7))は導けません。実は、ガリレイ変換の相対論版が回転変換(ローレンツ変換) だったように、今回求めたガリレイ変換のネーター保存量の相対論版は、4 元の正準角運動量の成分(M01,M02,M03 ) です。その保存性は時空の回転対称性(ローレンツ対称性) を必要とします。
《(第2版には無い)第6版で加えられた文》
「ベクトル(14.6)の成分は、どんな4元ベクトルの空間成分にもならない。・・・したがって、同じ粒子の系の重心も、基準系が異なれば、異なる(世界)点になるのである。」
以下で、この記述が誤りか正しいかを考察する。(「重心位置=4元ベクトルに係る量+4元テンソルに係る量」で定義されていると考えれば、その通りであると理解できると思いますが、、)。
こういう考察をすることが、これから研究者になろうとする人の研究活動の入り口だと思う。
先ず、2つの粒子の初期の位置が一致する場合は、ベクトル(14.6)で与えられる重心の位置は、ローレンツ変換によって、動径4元ベクトルとして変換される点(4元ベクトルの空間成分)になることを示す。

上図の静止した静止系Kに対して、そのx軸方向に速度vで動く慣性基準系K’を考える。静止系Kのt軸の線は世界線であり、その線上の点は世界点である。世界点は動径4元ベクトルであらわされる。ここで、静止質量mの粒子がある方向に速度wで運動し、静止質量Mの粒子が、その反対方向に速度nで運動するものとする。そして、静止系Kでの2粒子の重心が静止系Kの原点に(t軸という世界線上に)ある場合を考える。
この重心は静止系Kのt軸上にあるが、慣性基準系K’でみた重心位置はどうなるか。慣性基準系K’で見ても、この2粒子の重心が、x方向に速度-vで運動する静止系Kの原点位置に留まるか否かを調べる。もし、慣性基準系K’での重心位置も、静止系Kの原点位置に留まるならば、重心位置は静止系Kの原点位置という動径4元ベクトルの空間成分であることになる。
以下で、慣性基準系K'での、この2粒子の重心の運動速度を計算する。2つの粒子の初期の位置を、慣性基準系KおよびK'の共通の原点にあるものとする(その後、慣性基準系K’の原点は移動する)。すなわち、初期状態では2粒子の重心は静止系Kの原点にある。重心の位置の移動量は、重心の速度(ベクトル)に慣性基準系K'の時間t’を掛け算することで得られるので、重心の速度を調べるだけで重心の位置も定まる。
先ず、速度wで運動する質量mの粒子の慣性基準系K’で観測した速度を計算する。速度の合成の定理から、以下の速度が得られる。

次に、速度nで運動する質量Mの粒子の慣性基準系K’で観測した速度を計算する。(ただし、速度ベクトルnの方向は、負の方向であるものとする)。速度の合成の定理から、以下の速度が得られる。

次に、慣性基準系K'で観測されるJの式を計算する。

次に慣性基準系K'で観測される2粒子の総質量MT=ΣE/c2を計算する。

次に慣性基準系K'で観測される2粒子の重心のx方向の速度を計算する。

重心のx方向の速度は、慣性基準系K’で観測した静止系Kの原点の速度と同じである。
次に慣性基準系K'で観測される2粒子の重心のy方向とz方向の速度を計算する。

以上の計算の結果、2粒子の重心は、静止系Kの原点位置と同じ速度で運動し、重心位置は静止系Kの原点位置に留まることがわかった。
よって、慣性基準系K'での、世界線が交差する2粒子の重心の位置は静止系Kの原点位置に留まり、重心の位置は、静止系Kの原点の世界点をあらわす動径4元ベクトルの空間成分である。2粒子の世界線が交差する場合は、2粒子の相対運動の角運動量が無く0である場合である。
しかし、静止系Kでの2つの粒子の初期位置が静止系Kの原点位置に無い場合は、以下のようになる。
静止系Kでの2つの粒子のt=0の時点での位置が、その2つの粒子の重心が静止系Kの原点になる以下の座標位置にある場合を考える。(以下の式のパラメータχは時間の次元を持つ)。

速度wで運動する質量mの粒子のt=0における世界点の、 慣性基準系K’での時刻t’と位置とを計算すると以下の式の結果が得られる。

ここで、この粒子が速度w’で運動することを補正し、時刻t’=0でのこの粒子の位置を計算する。

一方、速度nで運動する質量Mの粒子のt=0における世界点の、 慣性基準系K’での時刻t’と位置とを計算すると以下の式の結果が得られる。

ここで、この粒子が速度n’で運動することを補正し、時刻t’=0でのこの粒子の位置を計算する。

時刻t’=0でのこの2つの粒子の重心を計算する。

この重心のx座標だけでも、静止系Kの原点(静止系Kでの重心)のx座標と一致することには、救いがあると思う。


こうして慣性基準系K’で計算した2つの粒子の重心位置は、2つの粒子の世界線同士が交差しない(角運動量が0で無い)場合は、時刻t’=0において、(静止系Kの原点と重なる原点を持つ)慣性基準系K’の原点にはなくΔy,Δzずれる。すなわち、慣性基準系K’で観測した重心は、静止系Kの原点に来ない。ただし、その重心も、静止系Kの原点(静止系での重心)と同じ速度vで移動する。
このように、回転する2粒子の、慣性基準系K’での重心位置の世界点は、静止系Kにおける重心位置の世界点と異なってしまう。
特に、静止系Kで下図左のような十字架棒が光速度に近い速度で回転している場合、x方向にその速度に近い速度vで進む慣性基準系K’から観測すると、その十字架棒は下図右のような形で運動していることが計算できた。

慣性基準系K’で観測すると、回転する十字架棒が上図の右のような形に歪んでいるなら、その場合の重心位置は確かに静止系Kの位置からY方向にずれた位置に移動すると考えざるを得ない。
場の古典論の第6版で、「重心位置がどんな4元ベクトルの空間成分にもならない」と言うのは、このことを指していると考える。以上の計算の結果、場の古典論の内容は誤っていない、と理解できる。
もう1つのモデルとして、静止系Kで、正電荷の粒子と負電荷の粒子の対が光速度に近い速度で回転しつつ静電気の引力(及び磁界によるローレンツ力)と遠心力でバランスを保って、粒子対の間隔が一定値に保たれている。それを光速に近い速度vで運動する慣性系K’で観測したモデルを考える。(金の原子では1s軌道の電子が光速度の半分くらいの速度で原子核の周りを回っているので、その電子の回転運動を考えた方が良いかもしれない)。その粒子対は、慣性基準系K’では、下図の右から左の順に推移して回転する。(ただし、絶えず光速度に近い速度ベクトルの方向を変えて運動する電荷が発生する電束の形と磁束の形を求めるのは難しい。)

上図のように、正電荷と負電荷の対が回転するモデルでも、粒子対の回転の形が歪む問題を生じる。
下に動作のアニメーション(通信データは消費しない)を示す。
回転十字架などのモデルが回転する場合に、静止系Kでは原点を中心にした形が回転対称な形に保たれるが、慣性基準系K’では、回転物体の重心が速度ーvで運動し、回転運動が歪んだり、物体の重心位置がずれる。それは、時空のゆがみによる現象だと考える。また、「回転物体全体を速度vで運動するように加速すると、やはり、時空の歪みにより、その加速方向に垂直な方向に重心が移動する」と解釈する。
《角運動量4元テンソルが重心の謎を解くカギだ》
この重心位置の不思議な振る舞いを理解するために、以下で、角運動量4元テンソルの意味を考察する。
先ず、角運動量4元テンソルを1つずつ書くと以下の式になる。以下で用いるベクトルΔを、重心位置変位ベクトルと名付ける。

《角運動量4元テンソルの行列》
角運動量4元テンソルをまとめると以下の行列になる。

4元テンソルは、ローレンツ変換によって、動径4元ベクトルの積のように変換される。そのため、慣性基準系の静止系K(ct,x,y,z)とそれに対してx軸方向へ速度vで運動している慣性基準系K'(ct',x',y',z')の間では、角運動量4元テンソルの各成分が、(6節の問2の解のように)以下のようにローレンツ変換される。(後に23節で学ぶ電磁場テンソルの各成分と同様に変換される)。

この式を解くと以下の式が得られる。

重心位置変位ベクトルΔは、ローレンツ変換によって、4元ベクトルとは異なって変換され、慣性基準系毎に異なる世界間隔のベクトルに変換される。
《回転する粒子対の角運動量4元テンソル》
角運動量4元テンソルは、回転する正電荷・負電荷対のモデルの場合には以下のようになる。(回転の半径をrとし、粒子の静止質量をmとする)。ローレンツ変換した後の、慣性基準系K'での角運動量4元テンソルが表す角運動量も、静止系Kでの角運動量4元テンソルが表す角運動量も時刻t=0における同じ原点(同じ世界点)を中心にした角運動量を表す。


静止系KでのテンソルMと、慣性基準系K’での(以上の式でローレンツ変換した結果の)テンソルM’とは、以下のテンソルになる。

《重心位置変位成分Δのローレンツ変換》
回転する物体の重心位置は、
(基礎重心位置ベクトル)+(重心位置変位ベクトルΔ) ,

であらわせると解釈できる。ここで、基礎重心位置ベクトルは4元ベクトルである。
そのように、回転する物体の重心が、基礎重心位置ベクトルから、(4元テンソルの成分に係る)重心位置変位ベクトルΔの分だけずれていると解釈できる。
ここで、速度ベクトルvで運動する慣性基準系K’での重心位置変位ベクトルΔが、静止系Kでの重心位置変位ベクトルからずれる差のベクトルが、以下の式で計算できる。(以下の式で、回転する物体の(静止系Kでの)角運動量ベクトルをMとする)。

(この位置のずれの大きさは、回転半径rの(w/c)(v/c)倍である。)
結局、回転する物体の重心位置の世界点は純粋な4元ベクトルではあらわせない。速度ベクトルvで運動する慣性基準系K’では、重心位置が、静止系Kでの重心位置とは異なる。その重心位置の差のベクトルが上の式であらわされる。
1個の電子でさえも回転している。そのため、電子の重心位置も、慣性基準系K’では、静止系Kとは異なる位置に変わる。
《角運動量成分のローレンツ変換》
また、先の、静止系Kの原点を中心にして回転する正電荷・負電荷対の角運動量Mは、慣性基準系K’で観測すると、ローレンツ変換によって角運動量テンソルM’に変わる。また、慣性基準系K’では、その正電荷・負電荷対の重心位置が静止系Kの原点位置からずれる。そのため、慣性基準系K’では、その原点(静止系Kの原点と同じ)に対して速度vで運動する正電荷・負電荷対の全質量の角運動量が生じる。それが、重心を中心にした、正電荷・負電荷対の角運動量に加わる。その総和が、原点(静止系Kの原点と同じ)を中心にした正電荷・負電荷対の角運動量として観測される。慣性基準系K’で観測する、原点を中心にした角運動量と、重心を中心にした角運動量を計算して以下の式を得た。
〔角運動量〕速度vで運動する慣性基準系K’での角運動量

(ただし書きの意味:4元テンソルには、4元ベクトルとは異なるローレンツ変換での不変量がある)
上の結果では、角運動量4元テンソルを使わないで計算した結果と、角運動量4元テンソルを使った結果が一致した。
静止系Kで観察した回転物体の角運動量が、慣性基準系K’で観察すると、値が変わる。そのため、粒子対の運動を、物体の重心系K=静止系Kでは円運動に維持させつつ、回転する粒子対全体を、慣性基準系K’で観測すると、速度vで運動するように加速するためには、粒子対に回転モーメントも加わえなければならないことになる。回転物体を相対論で扱うのは難しい。
なお、量子力学では、角運動量は量子化されてはいるが、ランダウの物理学小教程「量子力学」の32ページを見ると、角運動量などの物理量は量子化されていても、各固有値の波動関数を重ね合わせた波動関数には、平均値の物理量(値が連続的に変わる)が対応する。そのため、連続的な値の角運動量Mを考えることができる。
また、ディラック方程式の解説を見ると、以上での結論の「観測する慣性基準系K’ごとに角運動量M’の値が連続的に変わる」ことを否定しているわけでも無いように見える。(ディラックの波動関数の確率密度が、ローレンツ変換される4元ベクトルを構成する(7.127))。量子力学でも、慣性基準系K'で観測される角運動量M’は、静止系Kの角運動量Mから、角運動量テンソルの変換規則に従って変換されると考える。
《角運動量4元テンソルの解釈》
慣性基準系K’の角運動量4元テンソルM’は、以下の成分からなるテンソルであると理解できる。
(1)物体の重心位置が原点からずれる重心位置変位ベクトルΔに係る成分を持つ。重心位置変位ベクトルが生じる原因は時空の歪みだと考える。
(2)(静止系Kの原点を中心にした慣性基準系K'の角運動量)=(物体自身の重心を中心にした角運動量)+(物体全体が原点に対して回転する角運動量)=(値がずれた角運動量)が慣性基準系K'の角運動量の成分となっているように観測される。
(3)角運動量4元テンソルM’の成分は4元ベクトルの成分ではない。角運動量4元テンソルM’の成分は、23節の電磁場テンソルの成分と同様にローレンツ変換される。
(物理的意味を考える:電荷の中心もずれて見える?)
1つの物体が持つ電荷は、物体が運動しようがしまいが電荷の量に変わりはない。静止系Kで回転している物体を慣性基準系K’で観測すると重心位置がずれて見える。回転十字架の歪み具合からすると、物体中に分布する電荷の中心位置も、慣性基準系K’が異なれば、重心といっしょに、以下のように移動するだろうと考えられる。(思考実験1)静止系Kで、物体Aと物体Bが重力で引き合っているのを、静電気が打ち消して、互いの位置が変わらないバランスを保っているとする。それを慣性基準系K’で観測しても互いの位置が変わらないバランスを保っていることは同じである。慣性基準系K’が異なる場合でも、重心を中心にして対向する物体Aと物体Bが重力で引き合うならば、物体Aと物体Bが重心位置と同じ位置を中心にして静電気で反発し合って重力を打ち消してバランスが保たれると考える。静電気の場と重力の場は、同じローレンツ変換の式に従って変換されると考える。そのため、重力の中心が慣性基準系K’に応じてずれるならば、(電気力線の束の形も歪むので)静電気の中心も同じ様にずれて見えると考える。
(もっと深刻な問題がある)
回転物体の重心位置の世界点が、慣性系ごとに異なるという問題は深刻な問題だと思う。重心の世界点の位置が観測系ごとに異なるというのは、回転する粒子の位置(重心)が確定しないと解釈でき、深刻な問題があると思う。 「回転する2粒子の重心がずれるのは、粒子同士を引き付ける力の場の質量が計算に入っていないからだ!」という反論を検討するために、2粒子を紐で結んで回転させている下図の第3のモデルを考えた。

しかし、紐を含む全体が慣性基準系K’の原点から上方向(Y方向)に移動するので、紐の重さを考えたとしても、重心が原点からずれることは避けられない。
位置が確定しない問題を改善するためには、運動量が確定していることも疑った方が良いかもしれない。しかしながら、問題はそれだけでは無い。正電荷・負電荷対の回転モデルには、水素原子の陽子・電子対の回転モデルと同じ、もっと深刻な問題がある。正電荷を持つ粒子と負電荷を持つ粒子が重心を中心にして回転するならば、その電荷の移動・振動に伴い電磁波が発生する。その電磁波が発生する結果、粒子対は回転運動のエネルギーを失い、速やかに一体化して電荷が中和されるハズである。そのような不安定なモデルを前提にした粒子対の運動を計算して良いのだろうか?そもそも、水素原子をはじめとする原子が、原子核と電子が回転運動をしているのに、なぜ崩壊しないで安定しているのだろうか?
《時空の歪みの補正》
光に近い速度Vで運動している正電荷・負電荷対が歪んだ回転運動をしているとき、この粒子対を代表する点の位置は、時空の歪みを補正して、値を4元ベクトルにした以下の位置座標を使う方が良さそうに思える。

すなわち、測定した物体の重心位置を(物体の重心と同じ速度Vで運動する慣性系で観測した、物体の角運動量Mと運動質量m)を使って補正する。この補正により、慣性基準系K’で計算した重心位置から、静止系Kでの重心の位置が求められる。この補正により、時空が歪んで見える歪みの誤差を小さくできるだろうと考える。
なお、この問題で悩みすぎて時間を費やすよりも、角運動量が量子化されていると教える量子力学をしっかり勉強することに時間を使った方が良いと思う。
(想像力をふくらませて物理的意味を考える)

このモデルで、m=Mとし、(慣性基準系K’の速度ベクトルv)=(粒子の運動速度ベクトルw=-n)とし、慣性基準系K’は粒子mの速度ベクトルwと同じ速度ベクトルvで運動するものとする。特に、粒子同士が弱い重力場で引き合うのを電荷により反発して打ち消す弱い電荷が粒子に帯電しているものとする。
そして、速度vが光速度cに極めて近く、βが1/100くらいに小さいものとする。そうすると、静止系Kでの2粒子の総質量は200mぐらいで大きい。速度vで運動する慣性系K’で見た2粒子の質量は20000mに(静止系Kでの質量の100倍)大きくなる。速度vが更に光速度に近づくと、慣性系K’で見る質量は更に、静止系Kでの質量よりも大きくなる。その質量の大部分は、慣性系K’の運動する方向と反対方向進む粒子Mの質量が運動によって大きくなることで大きくなる。速度Vが十分に光速度cに近づくと、慣性系K’で見る粒子Mの運動質量がいくらでも大きくなると考えられる。粒子Mの運動質量がそれほど大きくなる場合に、その粒子Mからの大きな重力で粒子mが引き寄せられるのではないか?
その答えは以下のように考える。重力の大きさは、(電磁場と同様に)粒子の運動の方向ではあまり大きくならずに、粒子Mがとても大きな運動質量を持っても、その粒子Mと粒子mが帯電した電荷の電場を介して反発し合う力と釣り合う大きさの重力場しか生じないと考える。
(想像力をふくらませて物理的意味を考える(2))
もう1つ考える。自分が回転すると世界全体が回転して見える。自分は世界の中心にいるものとする。回転している自分から見える世界の変わりざまは、世界全体が自分に対して回転することにより生じる現象と考える。自分から十分遠方の点は光速度で回転運動していると見える。それより先はもっと早い速度で回転運動している。それでも大丈夫なのは、空間の歪みのためだと考える。自分から等速直線運動をして遠ざかっているものも、自分から見ると、自分の回りを回転するらせん運動をしながら自分から遠ざかっていくように見える。等速直線運動がそうなってしまうのも、空間の歪みによるものと考える。自分が、更に、光速度に近い速度Vで等速直線運動をすれば、回転している世界が、-Vの速度で自分に対して運動する運動が加わって運動するように見える。しかも、その-Vの速度の運動は、絶えず速度-Vの運動ベクトルの方向を変える運動になる。世界は回転しながら、その運動プラス、(絶えず向きを変えるが)-Vの速度の運動をする。世界の全ての物体の重心は、角運動量Mを持つ世界の物質が-Vで運動するので、-Vで運動する前の重心位置(自分の位置)からずれている。しかし、そのずれた世界の重心位置は、自分を中心にして回転運動して絶えず位置を変えると思う。そのような運動なので、そのように位置を変える重心を中心にして世界の角運動量を計算する意味は無いと思う。世界の角運動量は自分の位置を中心にして計測すべきだと思う。同じ様に、速度Vの運動物体の角運動量も、運動物体の重心を中心にして計算するのでは無く、静止系での物体の重心位置を中心にして計算すべきと思う。回転運動が歪んだり、物体の重心位置がずれるのは、時空のゆがみによる現象だと考える。
【リンク】
空間の等方性に起因する保存量としての角運動量
pdf 古典力学 (解析力学)
東京大学数理物理学班「古典力学」
「高校物理の目次」
ベクトルの外積の3重積の公式
【3重積の公式の証明(その1)】
「エディントンのイプシロン」(レビチビタ記号とも呼ばれる)を使って3次元ベクトルの外積を定義し、その3次元ベクトルの外積の3重積を計算することで、3重積の公式を楽に導出して思い出せるようになります。
3次元ベクトルAとベクトルBの外積でベクトルHを計算する式は、エディントンのイプシロンを使って:
εmprambp=hr
(この様に書く場合は、通常は、アインシュタインの縮約記法による積の和を表しています)
と表して覚えた方が覚えやすいです。
また、3次元ベクトルAとBの内積は、クロネッカーのデルタ
δst
を使って以下のように表すことができます。
ここで、以下の、3次元ベクトルAとBとCの外積の3重積を計算します。
この式の計算は、エディントンのイプシロンを使って、アインシュタインの縮約表記で以下のようにあらわすことができます。
この式で出て来た、3次元ベクトルに関する2重のエディントンのイプシロンは、以下の様に展開できます。
先ず、値が0にならない場合を先に列記します。
そのため、2重のエディントンのイプシロンを表すテンソルγstijは、クロネッカーのデルタδの積の差の以下の式と等価です。
この公式を使うと、以下の様に計算を進めることができます。
(証明おわり)
この、3次元ベクトルの外積の3重積の展開公式は、
以上の、3次元ベクトルに関する2重のエディントンのイプシロンの、クロネッカーのデルタの積の差への変換公式を使って、速やかに導き出す様に覚えましょう。
【3重積の公式の証明(その2)】
(公式の検算)
3次元ベクトルの外積の3重積の展開公式は以下の図を書いて検算できます。
(検算おわり)
(公式の証明開始)
(1)
上の検算の結果:
ベクトルAがX方向のベクトルであり、
ベクトルBがY方向のベクトルである場合に、
ベクトルCがX方向のベクトルであってもY方向のベクトルであっても公式が成り立つ。
ベクトルCがZ方向のベクトルの場合も、結果が0になるので、公式が成り立つ。
よって、
ベクトルAがX方向のベクトルであり、ベクトルBがY方向のベクトルである場合は、
ベクトルCがどの方向のベクトルであっても公式が成り立つ。
(2)
ベクトルAがY方向のベクトルであり、ベクトルBがZ方向のベクトルである場合も、同様にして、
ベクトルCがどの方向のベクトルであっても公式が成り立つ。
(3)
ベクトルAがZ方向のベクトルであり、ベクトルBがX方向のベクトルである場合も、同様にして、
ベクトルCがどの方向のベクトルであっても公式が成り立つ。
(4)
以上の(1)から(3)の、ベクトルAとベクトルBを入れ替えた場合にも公式が成り立つ。
すなわち、(3)の場合のベクトルAとベクトルBを入れ替えた場合:
ベクトルAがX方向のベクトルであり、ベクトルBがZ方向のベクトルである場合も、同様にして、
ベクトルCがどの方向のベクトルであっても公式が成り立つ。
(5)ベクトルAがX方向のベクトルであれば、
ベクトルBがX方向の場合も、結果が0になるので、ベクトルCがどの方向のベクトルであっても公式が成り立つ。
(6)
以上の(1)と(4)と(5)より、
ベクトルAがX方向のベクトルであれば、
ベクトルBがどの方向のベクトルであっても、そして、ベクトルCがどの方向のベクトルであっても、公式が成り立つ。
(7)
以上の(6)と同様にして、
ベクトルAがY方向のベクトルの場合もZ方向の場合も、
ベクトルBがどの方向のベクトルであっても、そして、ベクトルCがどの方向のベクトルであっても、公式が成り立つ。
(8)
以上の(6)と(7)により、
ベクトルAがどの方向のベクトルであっても、
そして、ベクトルBがどの方向のベクトルであっても、
そして、ベクトルCがどの方向のベクトルであっても、
公式が成り立つ。
(証明(その2)おわり)
【3重積の公式の証明(その3)】
3重積の公式は以下の様に直交ベクトル系a,h,avを定義して計算して求めることもできます。
先ず、3重積の公式の左辺を計算します。
次に、3重積の公式の右辺を計算します。
式9と式10の値が一致するので、以下の式の3重積の公式が成り立つ。
(証明(その3)おわり)
その3の証明とほとんど同じ証明ですが、以下の形の計算を行って証明することができます。
(1)ベクトルAの方向の単位ベクトルをベクトルXとする。
(2)ベクトルAとベクトルBの張る平面上のベクトルで、ベクトルAに垂直な単位ベクトルをベクトルYとする。
(3)ベクトルXとベクトルYの外積をベクトルZとする。ベクトルZは単位ベクトルになる。
直交ベクトル系、X,Y,Zで、ベクトルA,B,C、が以下の図のように表せる。
このとき、以下の式1が成り立つ。
また、以下の式2が成り立つ。
式1のベクトルと式2のベクトルが等しいので式3の関係が成り立つ。
(証明(その4)おわり)
【ベクトルの外積同士の内積の公式】
また、以下の公式も成り立ちます。
《証明(その1)開始》
(証明(その1)おわり)
《証明(その4)》
また、上の公式は、ベクトルhを用いて以下の様に計算して証明することもできます。
下図のように、ベクトルAとベクトルBの外積を単位ベクトルhを使って表し、直交ベクトル系hとaとavを定義する。
そして、公式の左辺の式を、以下の様にベクトルCとベクトルDをベクトルhとベクトルaとベクトルavであらわして計算する。
次に、公式の右辺の式を、ベクトルCとベクトルDをベクトルhとベクトルAとベクトルBであらわして計算する。
式11と式12の値が等しいので、以下の式が成り立つ。
(公式の証明(その4)おわり)
《応用例》
この公式を応用すると、以下の定理が成り立つ。

電場と磁場をバランスさせる
「高校物理の発想の基本」
以下の図のような場合に、運動する電荷に対して、電場と磁場の力をバランスさせて力を打ち消すことができます。
以下の図で、磁場は紙面の裏側に向けて紙面に垂直にかかっているものとします。
この場合に、この電荷と同じ速度で運動する座標系でこの電荷を見たら、以下の図のように見えます。
(磁場Hが運動すると誘導電場Eが生じる現象は、「電磁場のローレンツ変換」の公式であらわされます。この公式の理論は大学の2年生以上にならないと学ばないようです。)
電荷が静止して見える座標系では、運動する磁場が発生する電場がもともとあった電場を打ち消す結果、合計した電場が0になります。
その結果、上下の金属板間の電圧も0になります。電圧は、運動座標系が異なれば異なって見えます。
【蛇足】
なお、もともとあった電場も運動することで発生する新たな磁場ΔHの大きさを計算すると、相対性理論による磁場Hの大きさの誤差程度の磁場ΔHの値になります。
誤差範囲内の値なので、この値が元の磁場Hに加わるかどうかは、何とも言えません。正確な事実を知りたい人は、大学でアインシュタインの相対性理論の電磁場への適用を勉強して下さい。
(磁場Hが運動すると誘導電場Eが生じる現象は、「電磁場のローレンツ変換」の公式であらわされます。この公式の理論は大学の2年生以上にならないと学ばないようです。)
【リンク】
「高校物理の目次」
エディントンのイプシロンと行列式とベクトルの外積
「エディントンのイプシロン」(レビチビタ記号とも呼ばれる)を使って行列式が計算できます。
また、「エディントンのイプシロン」を使ってベクトルの外積を定義することで、ベクトルの外積の計算が楽になります。
【行列式】
行列式により、ベクトルが張る平行四辺形の面積や、斜方体の体積が計算できます。
「行列式」は、行の数と列の数が同じ正方行列の場合に計算できるものです。
(2行2列の行列の行列式)
2行2列の行列の行列式は、
その行列の要素が構成する2つの縦ベクトルが作る平行四辺形の面積をあらわすという意味を持ちます。
上図の式が行列式の記号です。
2行2列の行列Astの行列式は、
エディントンの行列式の計算記号εmpを使って、アインシュタインの縮約記法であらわして、
εmpAm1Ap2=Σ(m=1,2;p=1,2){εmpAm1Ap2}
(左辺の様な式を書いた場合は、通常は、アインシュタインの縮約記法による積の和を表しています)
で計算します。
この計算に利用する行列εmpは、
m≠pの場合の、
ε12=1,
ε21=-1
であり、
それ以外の、m=pとなる場合の、
εmp=ε11=ε22=0
です。
エディントンの計算記号εmpを定める規則は単純であり、
(1) εmpの添え字の値が等しければ、その値が0であり、すなわち、0=ε11=ε22であり、
(2) また、
ε12=1であり、
(3) εmpの任意の2つの添え字を入れ替えると、その値の正負の符号が変わる、すなわち、-1=ε21である。
これは、εmpがεmprになっても同じ規則が成り立ちます。
εmpAm1Ap2
(この様に書く場合は、通常は、アインシュタインの縮約記法による積の和を表しています)
は、
ベクトルA:
(a1,a2)=(A11,A21)と、
ベクトルB:
(b1,b2)=(A12,A22)
の作る平行四辺形の面積をあらわすという意味を持ちます。
εmpAm1Ap2=εmpambp
となる右辺の式であらわした方が分かり易いかもしれません。
行列式を具体的に計算すると、
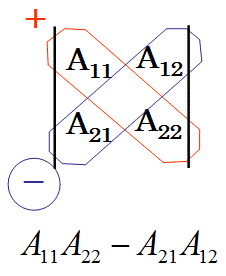
εmpAm1Ap2=A11A22-A21A12=a1b2-a2b1
です。
なお、行列式の計算方法は、行と列を入れ替えても変わらない、行と列に関して対称な式になっています。
すなわち、行列式は、以下の式でも計算できます。
εmpA1mA2p
(この様に書く場合は、通常は、アインシュタインの縮約記法による積の和を表しています)
(行列式は平行四辺形の面積)
以下で、行列式がベクトルの作る平行四辺形の面積を計算するものであることを説明します。
【第1の証明】
一言で言うと、行列式の計算式を見ると、
1列目のベクトルに垂直で長さが同じベクトルと、2列目のベクトルとの内積の計算であることがわかります。
ベクトルHを以下の式で定義してみます。
εmpam=hp
(この様に書く場合は、通常は、アインシュタインの縮約記法による積の和を表しています)
上の式でベクトルHを定義すると、
ベクトルHはベクトル(-a2,a1)になります。
そのベクトルHの長さは、ベクトルAと同じです。
ベクトルHとベクトルAの内積を以下で計算します。
すると、その内積は:
hpap=εmpamap=a1a2-a2a1=0
になり、0になります。
ベクトルHとベクトルAの内積が0になるので、ベクトルH、すなわち、hpはベクトルAに垂直なベクトルであることがわかります。
また、hpbp=εmpambp
(この様に書く場合は、通常は、アインシュタインの縮約記法による積の和を表しています)
となり、ベクトルHとベクトルBの内積が行列式をあらわします。
ベクトルAに垂直でベクトルAと同じ長さのベクトルHとベクトルBの内積は、 ベクトルAとベクトルBを斜辺とする平行四辺形OADBの面積ですので、行列式εmpambpの値は、その平行四辺形OADBの面積です。
(証明おわり)
これで証明ができましたが、以下の様な見方で考えるのも面白いと思うので読んでください。
(平行四辺形の面積の計算)
以下で、平行四辺形の面積を要素に分解して計算し、その要素を合計して平行四辺形の面積を計算します。
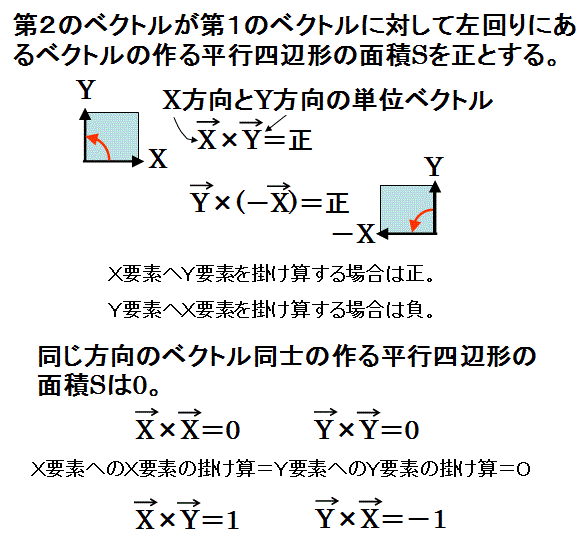
以下のように、座標系が回転しても結果が変わらないように面積の計算規則を定める点がポイントです。
X座標軸を反時計まわりに90°回転させてY座標軸に重ねると、Y座標軸は反時計まわりに90°回転してX座標軸の負の方向を向いて重なる。そのため、XベクトルとYベクトルの張る(ベクトルの順と成す角の向きを考えた)平行四辺形の面積を正にした場合、このように座標を回転させても面積が変わらないようにするには、必然的に、ベクトルの順と成す角の向きを考えた、Yベクトルと、X方向の負の方向を向いたベクトルの張る平行四辺形の面積を正にする必要がある。それは、YベクトルとX方向の正の方向を向いたベクトルの張る平行四辺形の面積を負にしなければならない事を意味する。
下図の様に、ベクトルAとBが平行な場合にベクトルAとBが張るつぶれた平行四辺形の面積は0である。
その平行四辺形の面積を、ベクトルAとBをそれぞれ、X方向のベクトルとY方向のベクトルの和で表し、その和のベクトルAとBの積を、X方向のベクトルとY方向のベクトルの積の和に展開して、以上で定めた計算規則に従って計算すると、その計算結果も0になる。
また、同じ方向を向くベクトルAとBが張るつぶれた平行四辺形は、その平行四辺形を回転させてどの方向を向かせても、同じ0の値の面積が計算できる。
平行四辺形を張るベクトルA及びBをX方向のベクトルとY方向のベクトルに分解すると、ベクトルAの分解されたベクトルとベクトルBの分解されたベクトルの積の組み合わせが作る平行四辺形が4個できる。その4個のうち2つの平行四辺形は、同じ方向のベクトルの張るつぶれた平行四辺形であり、その面積が0なので無視できる。
そして、その4個の平行四辺形の面積の和で、ベクトルAとBの張る平行四辺形の面積を計算したい。
上の例では、少なくとも面積が0のつぶれた平行四辺形の面積の計算では、その0の面積が、ベクトルAの分解されたベクトルとベクトルBの分解されたベクトルの積の組み合わせが作る4個の平行四辺形の和と同じになる演算ができる様になった。
次に、下図のように、ベクトルAとベクトルBの張る平行四辺形の面積を、同じ面積を維持するように高さを保たせて変形した平行四辺形にして面積を求める手法を、ベクトルAを分解したベクトルとベクトルBとの積の和を計算する手法に対応させて面積を計算する。
上図の、平行四辺形の変形と分解操作に対応するベクトルの積の式の分解操作の計算が以下の式であらわせる。
式0の様に、ベクトルAとベクトルBの(順番を考えた)積はそのベクトルAを分解した各ベクトルとベクトルBの張る各平行四辺形の面積の和に対応付けられる。
すなわち:
(ベクトルAのベクトルBに対する垂直成分の長さ)×(ベクトルBの長さ)
が平行四辺形の面積を表す。
一方、ベクトルAを分解して、
ベクトルA=ベクトルA1+ベクトルA2
とすると:
ベクトルA1のベクトルBに対する垂直成分の長さと、
ベクトルA2のベクトルBに対する垂直成分の長さの和は、
ベクトルAのベクトルBに対する垂直成分の長さに等しい。
そのため、
ベクトルAとベクトルBが張る平行四辺形の面積
=(ベクトルA1とベクトルBが張る平行四辺形の面積)
+(ベクトルA2とベクトルBが張る平行四辺形の面積)
の関係が成り立つ。
その関係は、
ベクトルA×ベクトルB
=(ベクトルA1×ベクトル B)
+(ベクトルA2×ベクトルB)
に分解した式で表すことができる。
すなわち、ベクトルが張る平行四辺形の面積についての分配法則に対応して、ベクトルの加法と(ベクトルの順番を考えた)乗法についての分配法則が共に成り立っている。
また、上図の様に、ベクトルAとベクトルBの張る平行四辺形を、
その平行四辺形を構成する2番目のベクトルBを、ベクトルAのk倍のベクトルを加えて、ベクトルAに対する高さを保たせて歪めたベクトルB2に変える。
そうして、ベクトルAとベクトルB2の張る平行四辺形を考える。
その場合、以下の式が成り立つ。
ベクトルの加法と乗法についての分配法則により、
ベクトルA×ベクトルB2
=(ベクトルA×ベクトルB)
+(ベクトルA×k(ベクトルA))
と表すことができる。
ここで、
(ベクトルA×k(ベクトルA))
は面積が0のつぶれた平行四辺形をあらわしているので、その面積は0である。
それゆえ、
ベクトルA×ベクトルB2=ベクトルA×ベクトルB
が成り立つ。
この式は、底辺の長さが同じで高さが等しい平行四辺形の面積が等しい事実と一致している。
この様に、平行四辺形の面積を表すベクトルの加法と乗法の分配法則が、変形した平行四辺形の面積の法則と一致して、成り立っている。
以上の演算規則で定めた、X座標方向の単位ベクトルとY座標方向の単位ベクトルが作る平行四辺形の面積の符号に合わせて、エディントンの計算記号εmpを定める。
それにより、ベクトルAの分解されたベクトルとベクトルBの分解されたベクトルの積の組み合わせが作る4個の平行四辺形の面積は、
εmpambp
で表せる。
その4個の面積要素の和を行列式と定義する。
エディントンの計算記号εmpは、以上で定めたX方向のベクトルとY方向のベクトルの積の値の正負の演算規則に合わせることで:
m=pとなる場合に、
εmp=ε11=ε22=0
にし、
m≠pの場合に、
ε12=1,
にし、
その添え字の順を入れ替えると符号が変わる、
ε21=-1
に定める。
その様にエディントンの計算記号εmpを定める。
その様に正負を定めた4つの平行四辺形の面積εmpambpの和をアインシュタインに縮約記法によって、
εmpambp=Σ(m=1,2;p=1,2){εmpambp}
とあらわして、
ベクトルAとベクトルBの張る平行四辺形の面積を計算し、その値を行列式の値にする。
その様にエディントンの計算記号εmpを定め、行列式の演算をεmpを使って定める事で、その行列式が、元のベクトルが張る平行四辺形の面積になる。
(平行四辺形の面積を1つ目のベクトルに垂直なベクトルと2つ目のベクトルの内積であらわす)
先に簡単に説明した事だが、念のため、以下で、このことを詳しく説明する。
三角形の面積Sは、以下の様に、ベクトルAに垂直なベクトルH=AvとベクトルBの内積であらわすことができる。
(式1’が平行四辺形の面積2Sの公式)
こうして得た式1’は、先に計算した行列式による面積の計算式1aと同じ式になった。
すなわち、2行2列の行列式は、ベクトルAに垂直なベクトルH=AvとベクトルBの内積であらわすことができる。
行列式はベクトルが張る平行四辺形の面積を表すが、その平行四辺形の面積は、ベクトルAに垂直なベクトルAvとベクトルBの内積でもあらわすことができる。そのため、行列式の計算を、ベクトルAに垂直なベクトルAvとベクトルBの内積の計算を表しているものと解釈して、行列式の計算から、ベクトルAに垂直なベクトルAvを導き出すことができる。
ベクトルBが、(b1,b2)であるとき、
行列式の値が、-b1a2+b2a1です。
ベクトルBとの内積がこの行列式の値になるベクトル(-a2,a1)を調べる。
このベクトルは、εmpamap=hpapとあらわしたベクトルH=hpであり、アインシュタインの縮約記法で:
hp=εmpam=Σ(m=1,2){εmpam}
となります。
このベクトル(-a2,a1)とベクトルA(a1,a2)の内積=0なので、
ベクトル(-a2,a1)は、ベクトルAに垂直であり、ベクトルAvに平行である。
しかも、ベクトル(-a2,a1)とベクトルBの内積が行列式の値と同じなので、
ベクトル(-a2,a1)=ベクトルAvである。
(注意)
hp=εmpam=Σ(m=1,2){εmpam}
ですが、
εmpap=Σ(p=1,2){εmpap}=-hm
になります。
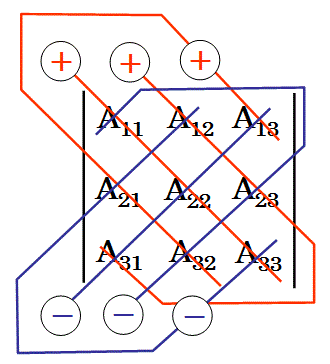
(3行3列の行列式)
3行3列の行列の行列式は、その行列の要素が構成する3つのベクトルAとBとCが作る斜方体の体積をあらわすという意味を持つ。
また、3つの3次元ベクトルの先端と原点とを頂点とする三角錐の体積は、その3つの3次元ベクトルを3つの列ベクトルとする行列式の値を6分の1にした値になる。
3行3列の行列Astの行列式は、
エディントンの行列式の計算記号εmprを使って、アインシュタインの縮約記法であらわして、
εmprAm1Ap2Ar3
で計算できる。
この計算に利用する行列εmprは、テンソルと呼ばれる。
(特に、物理学では、空間の位置座標をあらわすベクトル等の具体的な物理量を表すベクトルや、そのベクトルを変換する行列に、物理的意味を付けて呼ぶ。テンソルも、物理的意味の違いにより、テンソルか、擬テンソルと呼ばれる)
XYZ座標系での物理的長さを持つベクトルの張る斜方体の体積をあらわす行列式を計算するテンソルεmprは、擬テンソルと呼ばれる。
エディントンの計算記号εmprを定める規則は単純であり、
(1) εmprの添え字の値のどれかが等しければ、その値が0であり、
(2) また、
ε123=1であり、
(3) εmprの任意の2つの添え字を入れ替えると、その値な正負の符号が変わる。
という規則に従って、全てのεmprの値が定まる。
すなわち εmprは、m=p or m=r or p=rの場合に、
εmpr=0
であり、
m≠p、m≠r、p≠rの場合に、
ε123=ε231=ε312=1
であり、
上の要素の座標の添え字を入れ替えた場合の、
ε213=ε321=ε132=-1
という様に値を負にする。
なお、以下の様に添え字を入れ替えていくと、
ε231=ーε213=ε123=1
と変換して値が求められる。
εmprAm1Ap2Ar3
は、
ベクトルA:
(a1,a2,a2)=(A11,A21,A31)と、
ベクトルB:
(b1,b2,b2)=(A12,A22,A32)と、
ベクトルC:
(c1,c2,c2)=(A13,A23,A33)
の作る斜方体の体積をあらわすという意味を持つ。
行列式を具体的に計算すると、
εmprAm1Ap2Ar3
=A11A22A33
+A21A32A13
+A31A12A23
-A21A12A33
-A31A22A13
-A11A32A23
である。
(斜方体の体積の計算)
以下で、斜方体の体積を要素に分解して計算し、その要素を合計して斜方体の体積を計算する。
以下のように、座標系が回転しても結果が変わらないように体積の計算規則を定める点がポイントです。
以上の演算規則を定めることで、下図の様に、ベクトルAとBが平行な場合にベクトルAとBが張るつぶれた平行四辺形とベクトルCが張る体積0のつぶれた斜方体の体積を、下の式の様に、ベクトルを要素に分解した各要素ベクトルの体積の和で計算できる様になった。
上図の斜方体の体積を、ベクトルAとBをそれぞれ、以下の式で、X方向のベクトルとY方向のベクトルとZ方向のベクトルの和で表し、その和のベクトルAとBとベクトルCの積を、X方向のベクトルとY方向のベクトルとZ方向のベクトルの積の和に展開して計算すると、その計算結果も0になる。
上の計算により、同じ方向を向くベクトルAとBが張るつぶれた平行四辺形とベクトルCが張るつぶれた斜方体は、その斜方体を回転させてどの方向を向かせても、同じ0の値の体積に計算できる事が示された。
また、以下の計算により、体積が1の、ベクトルXとYとZの張る斜方体に、体積0の潰れた斜方体を加えていくと、ベクトル(-Y)とベクトルXとベクトルZの斜方体に変換できる。
これは、元の体積1の斜方体をZ軸のまわりに回転させた斜方体である。
また、例えば、以下の式の様に、ベクトルAとBとCが張る斜方体の体積を表す式に、ベクトルAとBと、ベクトルAのs倍とベクトルBのt倍の和のベクトルとが張る、体積が0のつぶれた斜方体の体積を表す式を加える。
式を整理すると、元の斜方体を張るベクトルCが、ベクトルAとBの張る平面に対する高さを維持して傾けたベクトルC’に変換され、ベクトルAとBとC’の張る斜方体の体積を表す式に変換される。
そして、そのように歪めた斜方体の体積は元の斜方体の体積と同じであるが、計算結果も同じ体積が計算できる様になった。
また、X方向のベクトルとY方向のベクトルの加法と乗法について分配法則が成り立つ。X方向のベクトルとZ方向のベクトルについても同様に分配法則が成り立ち、Y方向のベクトルとZ方向のベクトルについても同様に分配法則が成り立つ。その結果、全方向のベクトルの加法と乗法について分配法則が成り立つ。
ベクトルAとBとCが張る斜方体のベクトルCを2つのベクトルC1とC2の和に分解すると、
ベクトルAとBとCの張る斜方体の体積をVとし、
ベクトルAとBとC1が張る斜方体の体積をV1とし、
ベクトルAとBとC2が張る斜方体の体積をV2とすると、
ベクトルが張る斜方体の体積の間に
V=V1+V2
という関係が成り立つ。
一方で、
ベクトルA×ベクトルB×ベクトルC
=ベクトルA×ベクトルB×ベクトルC1
+ベクトルA×ベクトルB×ベクトルC2
というベクトルの加法と乗法についての分配法則が成り立つ。
斜方体として、
ベクトルA:
(a1,a2,a2)=(A11,A21,A31)と、
ベクトルB:
(b1,b2,b2)=(A12,A22,A32)と、
ベクトルC:
(c1,c2,c2)=(A13,A23,A33)と、
の3つのベクトルが張る斜方体を考える。
この斜方体を張るベクトルAとBとCをX方向のベクトルとY方向のベクトルとZ方向のベクトルに分解すると、ベクトルAの分解されたベクトルとベクトルBの分解されたベクトルとベクトルCの分解されたベクトルの積の組み合わせが作る斜方体が27個できる。そのうち21個の斜方体は、少なくも2つのベクトルが同じ方向を向いた3つのベクトルで張られるつぶれた斜方体であり、その体積が0であるため無視できる。その27個の斜方体の体積の和が、ベクトルAとBとCの張る斜方体の体積と同じになる演算ができる様になった。
そして、ベクトルAの分解されたベクトルとベクトルBの分解されたベクトルとベクトルCの分解されたベクトルの積の組み合わせが作る27個の斜方体の体積に係る、X方向の単位ベクトルとY方向の単位ベクトルとZ方向の単位ベクトルを組み合わせた積の符号を、エディントンの計算記号εmprを用いて定める。
この式でεmprを定義することで、
(1) εmprの添え字の値のどれかが等しければ、その値が0であり、
(2) また、
ε123=1であり、
(3) εmprの任意の2つの添え字を入れ替えると、その値な正負の符号が変わる。
という規則が成り立つ。
その規則に従うεmprを使うことで、ベクトルAの分解されたベクトルとベクトルBの分解されたベクトルとベクトルCの分解されたベクトルの積の組み合わせが作る27個の斜方体の各々の体積は、
εmprambpcr
で表せる(ここでは例外的にアインシュタインの縮約記法の積の和を使わず、1つの積のみを表す)。
その27個の体積要素の和を行列式と定義し、アインシュタインの縮約記法で、
εmprambpcr
と表す。
以上で、斜方体の体積を27個の体積要素に分解して計算し、その体積要素を合計して斜方体の体積が得られた。
そして、個々の単位ベクトルが張る斜方体の体積の和が、ベクトルAとBとCが張る斜方体の体積になるように、個々の斜方体の体積の正負を定める規則が、エディントンの行列式の計算記号εmprに反映されて定められている。
そのように、3階のエディントンの計算記号εmprを定める事で、3個のベクトルAとBとCが張る3次元の斜方体の体積が、各ベクトルを複数のベクトルに分解した場合の各ベクトルの張る複数の3次元の斜方体の体積の和になる。
すなわち、ベクトルの基本要素の3つの積で表される体積要素の3×3×3=27組の各体積要素の符号をエディントンの計算記号εmprを用いて定め、その27=33個の体積要素の和を、行列式にする。
こうして、エディントンの行列式の計算記号εmprを用いて表す、εmprambpcrによる計算を、3×3の行列式の計算規則とする。
その様に行列式を、εmprambpcrで計算する事に定める事で、その行列式が元のベクトルが張る斜方体の体積を計算する式になる。
(面に垂直なベクトルと残りのベクトルの内積で体積を求める)
この斜方体の体積は、ベクトルAとBに垂直で、大きさがベクトルAとBの張る平行四辺形の面積に等しいベクトルHとベクトルCの内積であらわすことができる。
そのために、
行列式の計算を、ベクトルHとベクトルCの内積の計算を表しているものと解釈して、
行列式の計算から、以下の様にしてベクトルHを導き出すことができる。
εmprambp=hrと表す。
ベクトルhrとベクトルAとの内積=εmprambpar=0であり、
(同じベクトルが並ぶ行列式の値は0であるため)
ベクトルhrとベクトルBとの内積=εmprambpbr=0です。
(同じベクトルが並ぶ行列式の値は0であるため)
そのため、
ベクトルhrはベクトルAとBに垂直である。
(補足)
同じベクトルが並ぶ行列式の値が0になることは、εmprを用いて以下の様に証明できる。
【証明開始】
εmpr=-εrpmであるので、
εmprambpar=-εrpmambpar
=-εrpmarbpam=-εmprambpar ,
∴ 2εmprambpar=0 ,
εmprambpar=0 ,
(証明おわり)
また、
ベクトルCが、(c1,c2,c2)であり、
行列式の値=εmprambpcr =hrcrであり、
行列式が表す斜方体の体積がベクトルhrとベクトルcrの内積の値に等しいので、
ベクトルhrの大きさは、ベクトルAとBの張る平行四辺形の面積に等しい。
以上の結果から、 εmprambp=hrは、
ベクトルAとBに垂直で、大きさがベクトルAとBの張る平行四辺形の面積に等しいベクトルHです。
ベクトルAとBに垂直なベクトルHを計算する上の式は、
ベクトルの外積の計算式:
ベクトルA×ベクトルB=ベクトルH
を表している。
ベクトルの外積の計算式は、上の式
εmprambp=hr
で覚えた方が覚えやすいです。
(念のため補足:この式はアインシュタインの縮約記法で表した積の和)
このように、エディントンの行列式の計算記号εmpを用いて表す行列式は、行列を構成するベクトルが作る面積や体積をあらわします。
(n行n列の行列式)
ε(p1)(p2)(p3)・・・(pn){A(p1)1A(p2)2A(p3)3・・・A(pn)n}
でn行n列の行列式を計算する。
このエディントンの計算記号の集合は、添え字が2つのものは行列と呼び、添え字が3つ以上のものと行列とは合わせてテンソルと呼ぶ。
このエディントンの計算記号ε(p1)(p2)(p3)・・・(pn)は、nn個の要素を持つが、
その各要素は、以下の値を持つ。
添え字のうちの少なくとも2つが同じ添え字になる場合、
ε(p1)(p2)(p3)・・・(pn) =0
であり、
ε(1)(2)(3)・・・(n)=1
であり、この添え字の位置を交換すると(-1)倍になる。例えば、1と2を交換すると、
ε(2)(1)(3)・・・(n)=-1
になる。
(備考)
ε1,2,3,4=1ですが、
ε2,1,3,4=ー1 ,
ε2,3,1,4=1 ,
ε2,3,4,1=ー1 ,
になり、添え字を1つづつずらして循環したら符号が変わります。
しかし、添え字の数を奇数にすれば、
1=ε1,2,3,4,5=ε2,3,4,5,1
のように、添え字を1つづつずらして循環したら符号が同じになります。
その様にn階のエディントンの計算記号εmp・・・を定める事で、n個のベクトルが張るn次元の斜方体の体積が、そのベクトルを複数のベクトルに分解した場合の各ベクトルの張る複数のn次元の斜方体の体積の和になる。
そして、斜方体を張るn個のベクトルをn次元の各座標軸方向のn個の要素のベクトルに分解して、n個の要素のベクトルをn組掛け合わせて体積を求める。
そのnn個の各要素の符号をエディントンの計算記号εmp・・・を用いて定め、そのnn個の体積要素の和を、行列式にする。その様に行列式を定める事で、その行列式が、元のベクトルが張るn次元の斜方体の体積をあらわす。
【行列式は行と列を入れ替えても結果が同じ】
行列式は、計算の元になる行列の行と列に関して対称な計算式です。そのため、行と列を入れ替えた行列でも行列式は同じ値になります。
紙面の平面内の2つのベクトルの外積
3Dゲームのソフトウェアを作るには、以下で説明する外積が必須知識だそうです。そのために外積を使うには、公式だけ覚えれば十分みたいですが。
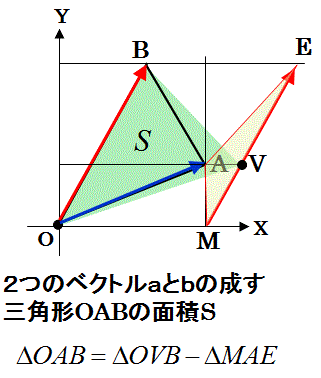
【課題】下図のように頂点の1つが原点Oにあり、他の2頂点が、A(a1,a2)とB(b1,b2)である三角形BOAの面積を計算する。
三角形の辺を成すベクトルを分解して、その分解したベクトルで作った複数の三角形の面積を足し算することで、三角形の面積を計算する。
上図のように、2つのベクトルの成す平行四辺形DBOAの面積をベクトルの掛け算(×)であらわします。
このベクトルの掛け算のことをベクトルの外積と呼びます。
(注意)
ベクトルの外積は、
「2つのベクトルどちらにも垂直な方向(この図の場合は紙面に垂直な方向)のベクトルを計算すること。そのベクトルの長さは、平行四辺形DBOAの面積にする。」
です。
平面(紙面)上のベクトルの外積を計算した結果は、いつでも紙面に垂直なベクトルで、その方向が変わることがありません。
そのため、先ずは、紙面上の2つのベクトルの外積による、紙面に垂直なベクトルの大きさの計算を行ない、ベクトルの外積の計算に親しむことにします。
三角形BOAの面積Sはこの平行四辺形DBOAの面積の2分の1です。
三角形BOAはベクトルOBとベクトルOAで作られる三角形です。
この三角形を作る2つのベクトルのうちの1つのベクトルOAを、下図のように、2つのベクトルに分解します。
すなわち、ベクトルOAを、ベクトルOM(単位ベクトルxのa1倍)とベクトルMA(単位ベクトルyのa2倍)に分解します。
上図のように、分解されたそれぞれのベクトルを使って2つの三角形を作ります。
1つ目の三角形は、ベクトルOM(単位ベクトルxのa1倍)とベクトルOBで作られる三角形BOMです。
2つ目の三角形は、ベクトルMA(単位ベクトルyのa2倍)とベクトルME(=ベクトルOB)で作られる三角形EMAです。
上図を見ると、その2つの三角形の面積の和が三角形BOAの面積になっていることがわかります。
ただし、ベクトルOMとベクトルOBで作られる三角形BOMは正の面積ですが、
ベクトルMAとベクトルME(=ベクトルOB)で作られる三角形EMAは負の面積を持つものとします。
この2つのベクトルで作られる三角形の面積が正であるか負であるかの区別は、三角形を作る2番目のベクトルが1番目のベクトルよりも左回りに回転した方向を向いていれば面積が正であり、右回りに回転した方向を向いていれば面積が負であるとして、区別します。
下図のように、それぞれの三角形を面積が同じ直角三角形に変形します。
三角形BOMは直角三角形NOMに変形し、
三角形AMEは直角三角形AMF変形します。
こうして、それぞれの三角形の面積を計算します。
以上のように、元の三角形を構成するベクトルを分解することで三角形を2つに分解して、その2つの三角形の面積の和で元の三角形の面積を計算することができることが確認できました。
なお、上図では、ベクトルOAをベクトルOMとベクトルMAに分解しましたが、ベクトルOAをその他のどんなベクトルの和に分解した場合でも、それらのベクトルが作る2つの三角形の面積の和は必ず三角形BOAの面積になります。
以上の計算は、以下の式のように単純なルールに基づいて計算できます。
(1)ベクトルxと、(同じ)ベクトルxが作る平行四辺形は1本の線分につぶれていますので、その面積が0です。
(平行な2つのベクトルが作る平行四辺形の面積は0です。)
(2)ベクトルの順番を入れ替えて外積を計算すると、そのべクトル同士の回転方向が逆回りになるので、面積の正と負が逆になります。
上のベクトルの外積の計算は、三角形BOAがどんな形の場合であっても計算結果が変わらず、
三角形の面積S=(a1b2-a2b1)/2 (式1)
となります。
すなわち、どんな三角形の場合でも成り立つ式(ただし、面積が負になる場合もありますが)です。
そのため、どんな三角形の場合でも上の式が成り立つことが証明できました。
上の式1でクロス積の形をした部分は、行列式とも呼ばれています。
(ベクトルの内積で面積をあらわす)
この三角形の面積Sは、ベクトルAを90度回転させたベクトルAvを使って、以下の様にあらわすことができます。
(式1’が三角形の面積Sの公式)
こうして得た式1’は、先に得た式1と同じ式になりました。