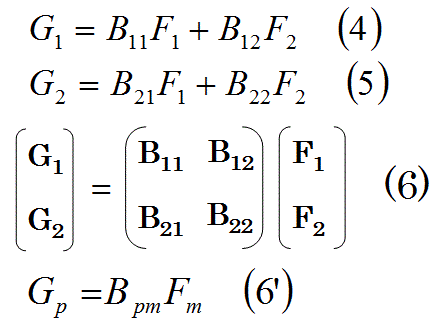アインシュタインの縮約記法
ベクトル解析の問題を解くとき、アインシュタインの縮約記法を用いると便利です。
以下の、「行列の掛け算の定理」を証明するという課題を解く例を参考にして、アインシュタインの縮約記法を説明します。
(条件1)ベクトルDが、以下の式1と式2によりベクトルFに変換されること。その式の係数が行列Aを成すこと。
式1と式2の演算の係数を添え字を付けて区別して式3で表します。
この式3は、式3’とあらわすと便利です。
この表し方はアインシュタインが提案した表記方法です(アインシャタインの縮約記法)。
この式3’は、変数で表した添え字の変数名が同じ場合に、その変数名の添え字のあらゆる場合(この場合は1と2のみ)について和をとることにした式です。
(条件2)ベクトルFが、以下の式4と式5によりベクトルGに変換されること。その式の係数が行列Bを成すこと。
式4と式5の演算の係数を添え字を付けて式6で表します。
この式6は、アインシュタインの縮約記法の式6’であらわせます。
式6’に式3’を代入すると式7が得られます。
式7は、更に式8に変形できます(式8はアインシュタインの縮約記法であらわした式です)。
式8’のように、演算Aと演算Bを合成した演算Cを考えます。
式8から、演算Cをあらわす行列Cの要素の値を計算する式9が得られます。
こうして、演算AとBの行列の要素を用いた式9で演算Cをあらわす行列Cの要素が計算できることがわかりました。
この演算Cを、式10のように、演算Aと演算Bの積(掛け算)と定義します。
そして、その演算Aと演算Bの掛け算である演算Cの行列の要素は式9’で計算できます。
これが、行列の掛け算の定理です。
すなわち、行列の掛け算の定理を、以下のようにあらわすことができます。
(条件1)ベクトルを式1~2でベクトルに変換する演算Aの行列Aが定義され、
(条件2)ベクトルを式4~5でベクトルに変換する演算Bの行列Bが定義されている場合に以下のことが成り立つ。
(結果)
第1のベクトルを演算Aで変換して第2のベクトルを得、更に、第2のベクトルを演算Bで変換して第3のベクトルを得る場合、
その2つの演算は、第1のベクトルを第3のベクトルに変換する演算Cにまとめることができる。
演算Cの行列Cは、式9’で計算することで求めることができる。
その演算Cを、演算Aに演算Bを掛け算した演算であると定義する。
演算Cの行列の要素を計算する式9’の計算を、行列の掛け算と定義する。
【計算の形】
なお、この掛け算の計算方式をベクトルAとBの内積にあてはめると、以下の形の行列の計算になる。
この計算は、横ベクトルAと縦ベクトルBの積であらわせる。
磁場の中を運動する平行平板に加わる力
【問】
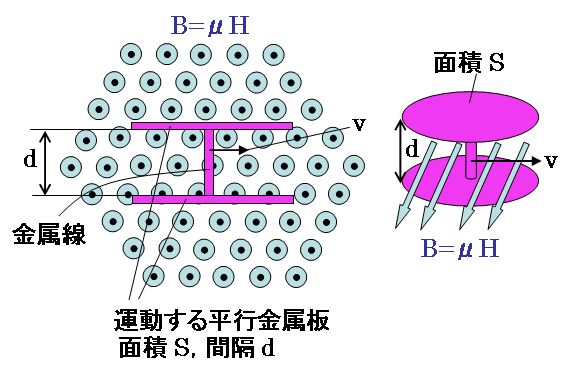
下図のように、紙面に垂直な面の金属の平行平板があり、その両方の金属板を金属線で接続しています。そこに、紙面から紙面の手前に向く磁場(磁束密度B)を加えます。
そして、その金属の平行平板を、平板の面の方向で磁場に垂直な方向に速度vで運動させます。
このとき、この金属の平板は電磁場からどのような力を受けるか。
平行平板の面積はSとし、平行平板の間隔をdとする。
【解1】
先ず、この問題を、平行平板といっしょに運動する運動座標系の観測者から観測される状況に基づいて解きます。
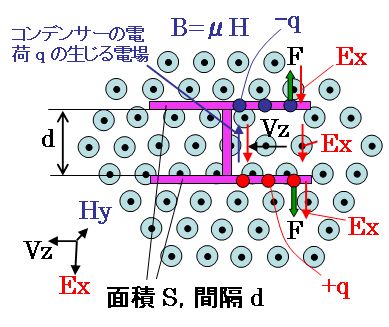
その座標系で観察すると、下図のように見えます。
磁場Hが速度Vzで運動するので、誘導電場Exが発生します。
その誘導電場Exが加わった金属の平行平板とそれをつなぐ金属線は、どこでも電位が同じになるように電荷が移動して空間から加わった誘導電場Exを打ち消す電場を発生させます。
それにより打ち消される金属板間の電圧は、Ex・dです。そのため、平行平板の両端には、平行平板に電圧Ex・dがあらわれるだけの電荷q=C・(Ex・d)がたまります。
金属の平行平板には電荷qがたまりますので、その電荷qには、対向する電荷からの電場が加わります。その電場の大きさは以下のように計算できます。
電荷qには、誘導電場Exと、対向する電荷からの電場とが加わり、その電場の合計が、以下のように、電荷qに力Fを及ぼします。
この大きさの力Fが、平行平板同士を遠ざける方向に加わります。
(解答おわり)
【解2】
次に、この問題を、磁場と一緒に静止している座標系の観測者の視点で解きます。
(この解き方の方が普通の解き方であると思います)
その座標系で観察すると、下図のように見えます。
速度vで運動する金属線に、単位長さあたりに起電力Eが発生します。金属板間の距離dでは、E・dの起電力が発生します。その起電力の電圧E・dが金属板間に加わります。
(磁場中における金属板間の電圧は、観測者の運動座標系が異なれば異なります)
平行な金属板は容量がCのコンデンサーを成すので、電圧E・dが加われば、その平行金属板に電荷q=C・(E・d)がたまります。
そうして溜まった電荷は平行な金属板と一緒に速度vで運動しますので、磁場からローレンツ力を、平行平板同士を遠ざける方向に、受けます。
電荷qには、ローレンツ力と、対向する金属板上の電荷の発生する電場(E/2)からの力を受けます。
その総和の力を計算すると、以下のようになります。
この大きさの力Fが、平行平板同士を遠ざける方向に加わります。
(解答おわり)
電磁気学のベクトル解析の目次
大学で学ぶ電磁気学のベクトル解析の全貌については、
が詳しいで参考にして欲しいと思います。
「ベクトル解析公式の証明-準備篇」も参考になります。
「レビチビタ記号とその性質」の簡潔な説明も良いです。
「Levi-Civitaの記号でベクトル解析の初歩を1」も参考になります。
以下では、大学で学ぶ電磁気学のベクトル解析の一部の、このサイトのオリジナルな説明のみの一覧を書きます。
【目次】
上の問題の様な電磁気学の問題を体系的に解けるようにする電磁気学のベクトル解析をやさしく学ぶコツを以下で考えていきます。
アインシュタインの縮約記法
紙面の平面内の2つのベクトルの外積
エディントンのイプシロンと行列式とベクトルの外積
ベクトルの外積の3重積の公式